- Solve simple problems
- Decomposition
- Pattern matching
- Abstraction
- Systems Analysis
- Identify the system parts and processes
- Use R to simulate a system
- See what happens in the long term
- See the effect of changing rates or initial conditions
May 12, 2020
Our course so far
Computational Thinking
We know that Computational Thinking has four parts
- Decomposition
- Pattern recognition
- Abstraction
- Algorithm design
Today we will talk about patterns
Patterns
in the dictionary
- a repeated decorative design: a wallpaper pattern
- an arrangement or sequence regularly found in comparable objects: the house had been built on the usual pattern
- a regular form or sequence discernible in certain actions or situations: the problems followed a repeated pattern
Science is about Patterns
- The goal of Science is to understand Nature
- We find the laws that explain Patterns in Nature
- The first step is to find Patterns
- Day & Night, Winter & Summer are Patterns
- Understanding seasons allows us to survive
- Some food makes us healthy
- Understanding which food makes us sick is essential to survive
Patterns in Technology


Patterns in Technology


Patterns in Nature


Patterns in Nature


Patterns in Nature


Patterns in Nature


Patterns in Art

Patterns in Decoration
Patterns in Music
Patterns in movement: repetitions
Patterns in programs
When we see a pattern we can make
- loops, if we need to repeat the pattern in one place
- Like drawing each angle in a star
- functions, if the pattern is used in several places
- Like drawing several stars in different places.
There is another kind of pattern
Recursive patterns in the Nature

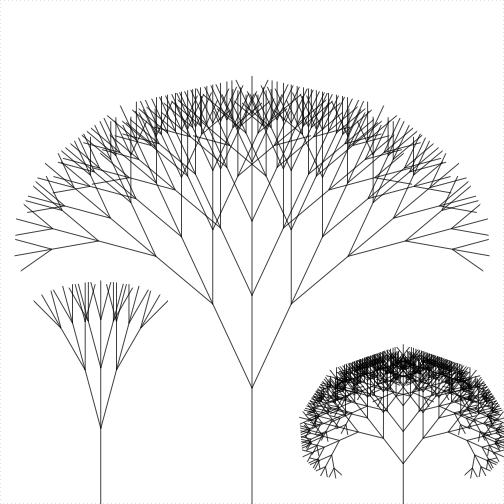
Recursive patterns in Trees

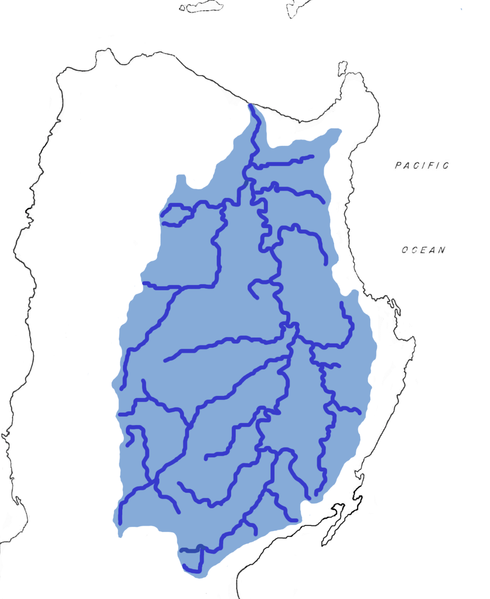
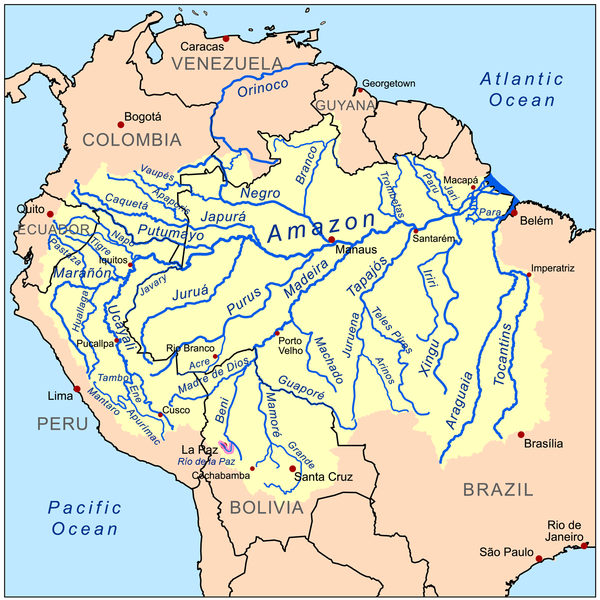
Recursive patterns in the Rivers
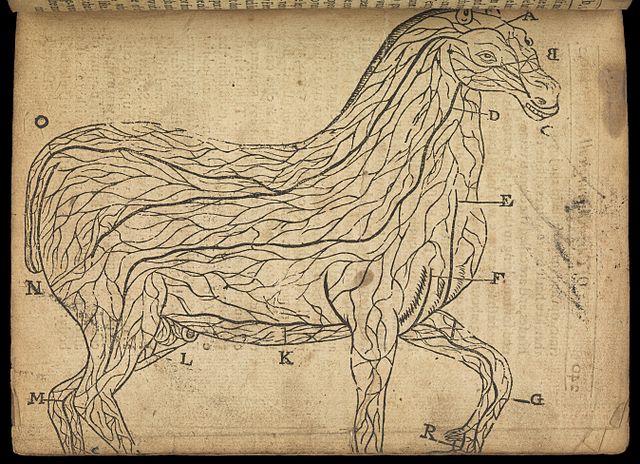
Recursive patterns in the Body
A Pattern can be part of itself
Sometimes the easiest way to define a pattern is to use the same pattern.
For example:
- A tree has a trunk and branches. Each branch is a trunk with branches.
- In other words, each branch is a little tree
- Real trees or phylogenetic trees
- Rivers are made of small rivers
- Blood vessels connect smaller blood vessels
Recursive functions
To represent these patterns we use functions that are part of themselves
example<-function(input) {
code
example(data)
code
return(output)
}

Example of recursive function
One useful mathematical function is factorial
The factorial of a \(n\) is \(n!\), defined as \[n! = n\cdot(n-1)!\]
That is, the factorial of n is n times the factorial of n-1
How do we write it in R?
Let’s write our own factorial function
factorial <- function(n) {
ans <- n * factorial(n-1)
return(ans)
}
There is an error here. Can you find it?
Use the debugger to see what is happening
factorial(4) visually
factorial(4) visually
factorial(4) visually
factorial(4) visually
factorial(4) visually
Exit condition
Each recursive function needs an exit condition
That is, some rule to decide when to finish
There is always an easy case that does not require recursion
For example, the factorial of 1 is \(1! = 1\).
Exit condition for factorial
factorial <- function(n) {
if(n <= 1) {
ans <- 1
} else {
ans <- n * factorial(n-1)
}
return(ans)
}
Correct factorial(4)
Example of recursive function to find minimum
find_min <-function(vector) {
n <- length(vector)
if(n==1) {
return(vector[1])
} else {
a <- find_min(vector[1:(n/2)])
b <- find_min(vector[(n/2+1):n])
if(a<b) {
return(a)
} else {
return(b)
}
}
}
find_min(c(12, 10, 15, 11, 13))
The simple cases return a single value
Then the “parent” chooses between two options
Then once again…
…and we get the final value
Another Example
tree <- function(level) {
save turtle position
if(level<=1) {
draw branch
} else {
tree(level-1)
}
recover turtle position
}
Improved Example
- Branch color depends on level
- Line width depends on level
- Lower levels have smaller length
- Branch angle changes with level

Online material
“In order to understand recursion, one must first understand recursion.”
How Recursion Works — explained with flowcharts and a video
Exercise: Homework from previous year