1. Algorithm design

In many important cases we have a vector x with growing values. That is, each value is bigger or equal to the previous one, and x[i+1] >= x[i] for all i indices. The official name is monotonic increasing.

It is easy to see that the minimum value has to be at position 1. We also know that the maximum value is at the last position. What about the half value?

The half value is the average of the minimum and the maximum. For example if x is the vector c(1, 4, 4, 6, 10, 15) then the half value is (1+15)/2, that is 8.

The location of the half value of the vector x is the index of the first value that is equal or bigger than the half value of x. In the example the location of the half value is 5, since x[5] is the smallest value that is bigger or equal than 8.

Please write a function called locate_half(), with one input called x. The function must return a single number, which is the index of the smallest value in x that is bigger than or equal to the average of minimum and maximum of x.

You can test your functions with the following code. The output should be this:

x <- 1:9
locate_half(x)

## [1] 5

locate_half(x + 20)

## [1] 5

locate_half(x * x)

## [1] 7

locate_half(sqrt(x))

## [1] 4

2. Trees and branches

Trees are a common recursive structure found in nature. Each branch is like a small tree. More precisely, a tree with n levels has branches with n-1 levels. Your task is to make a function to draw trees with three branches.

The function should be named tree() with three inputs: the number of levels n, the length of the trunk length, and the angle between the branches angle. Each branch is a tree with n-1 levels and with length equal to 0.8 times the length of the previous level. The first branch of every tree is angle degrees to the left of the trunk; the second is aligned with the trunk, and the last one is angle degrees to the right of the trunk.

The most important issue is that the tree() functions must leave the turtle in the same position and the same angle as before. Your function can move the turtle as you wish, but it must leave the turtle as it was at the beginning of the function. The functions turtle_getpos(), turtle_getangle(), turtle_setpos(), and turtle_setangle() can be useful for this.

You can test your function with the commands

library(grid)
library(TurtleGraphics)
turtle_init(mode="clip")
turtle_hide()
turtle_setpos(50,0)
tree(6, 23, 25)
turtle_setpos(20,0)
tree(4, 15, 15)
turtle_setpos(80,0)
tree(7, 8, 38)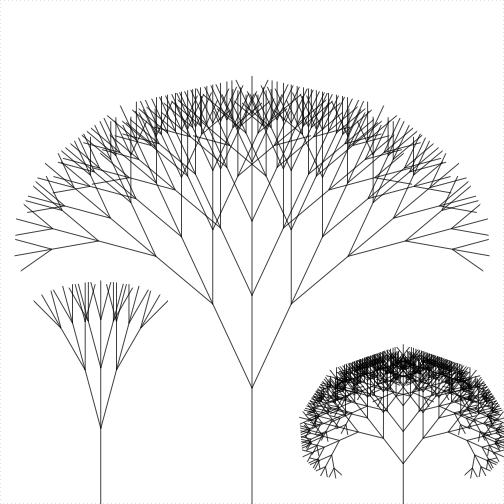

Figure 1. If you did it right, you should get this picture

Extra points: Modify the tree() function to make the width of each branch part equal to the level. Can you change the color of each part, like in the Figure 2?