Class 31: Central Limit Theorem
Methodology of Scientific Research
Andrés Aravena, PhD
18 May 2023
Francis Galton, his cousin and his machine
Francis Galton

English explorer, Inventor, Anthropologist
(1822–1911)
Francis Galton
- Cousin of Charles Darwin
He studied medicine and mathematics at Cambridge University.
He invented the phrase “nature versus nurture”
In his will, he donated funds for a professorship in genetics to University College London.
Galton Machine
Simulated Galton Machine
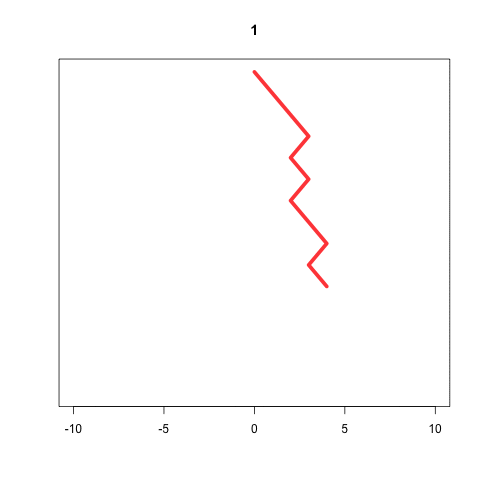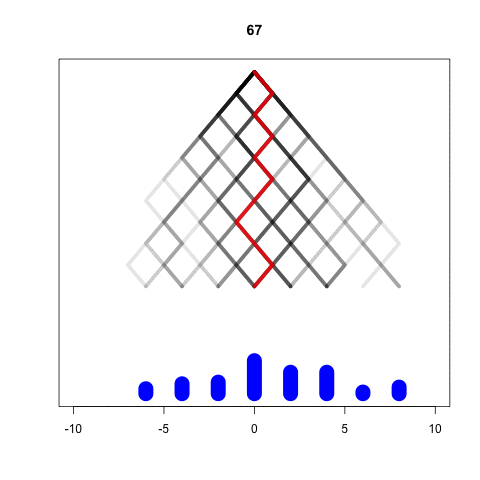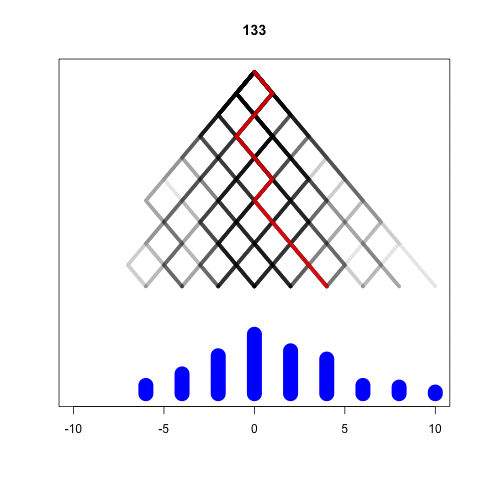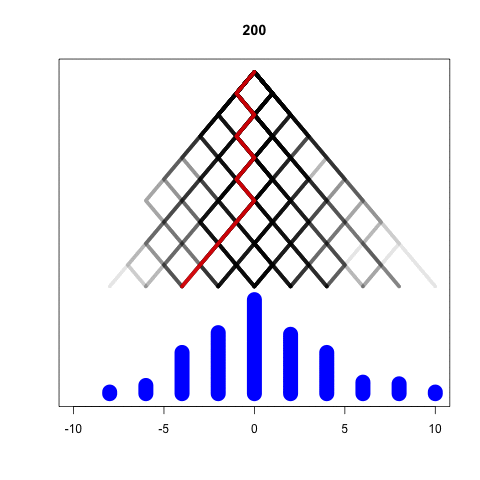
Simulating the Galton Machine
We take each ball independently
In every level, the ball bounces either left or right
We represent these options as -1 and 1
At the last level the position is the sum of all bounces
Simulating the Galton Machine (M=5)
Larger M, larger variance
Bigger M gives wider results

How Variance Grows (log–log scale)
What happens when 𝑛 is big?
A simple model
Now we have a coin 𝑋 with two possible outcomes: +1 and -1
To make life easy, we assume 𝑝=0.5
What are the expected value and variance of X ?
Throw the coin 𝑛 times
We throw the coin 𝑛 times, and we calculate 𝑌, the sum of all 𝑋 \[Y=\sum_{i=1}^𝑛 X_i\]
What are the expected value and variance of 𝑌 ?
It is easy to see that
- \(𝑌\) is basically a Binomial random variable
- \(𝔼 𝑌 = 0,\) because \(𝔼 𝑋 = 0\)
- \(𝕍 𝑌 = 𝑁,\) because \(𝕍 𝑋 = 1\)
Fix the variance to 1
Now consider \(Z_n=Y/\sqrt{𝑛}\)
It is easy to see that \(𝔼Z_n = 0\) and \(𝕍Z_n = 1\) independent of 𝑛
The possible values of \(Z_n\) are not integers. Not even rationals
What happens with \(Z_n\) when 𝑛 is really big?
Variance 1, M=5
Variance 1, M=50
Variance 1, M=500
Variance 1, M=5000
When M is big, we get a Normal distribution
The Normal distribution
This “bell-shaped” curve is found in many experiments, especially when they involve the sum of many small contributions
- Measurement errors
- Height of a population
- Scores on University Admission exams
It is called Gaussian distribution, or also Normal distribution
Normal distribution
Here outcomes are real numbers
Any real number is possible
Probability of any \(x\) is zero (!)
We look for probabilities of intervals
The Central Limit Theorem
“The sum of several independent random variables converges to a Normal distribution”
The sum should have many terms, they should be independent, and they should have a well defined variance
(In Biology sometimes the variables are not independent, so be careful)
Central limit theorem
When \(n→∞,\) the distribution of \(Z_n=∑ X/\sqrt{𝑛}\) will converge to a Normal distribution \[\lim_{n→∞} Z_n ∼ Normal(0,1)\]
More in general
If \(X_i\) is a set of i.i.d. random variables, with \[𝔼X_i=μ\quad\text{and}\quad 𝕍X_i=σ^2\quad\text{for all }i\] then, when \(n\) is large \[\lim_{n→∞} \frac{\sum_i X_i-μ}{σ\sqrt{𝑛}} ∼ \text{Normal}(0,1)\]
In other words
If \(X_i\) is a set of i.i.d. random variables, with \[𝔼X_i=μ\quad\text{and}\quad 𝕍X_i=σ^2\quad\text{for all }i\] then, when \(n\) is large \[\lim_{n→∞} \frac{\sum_i X_i-μ}{\sqrt{𝑛}} ∼ \text{Normal}(0, σ^2)\]
This is why Normal distributions are important
Noise is usually Normal
- Thermal noise is the sum of many small vibrations in all directions
- they sum and usually cancel each other
- Phenotype depends on several genetic conditions
- Height, weight and similar attributes depend on the combination of several attributes
It does not always work
- Not all combined effects are sums
- some effects are multiplicative
- Some effects may not have finite variance
- sometimes variance is infinite
- Not all effects are independent
- this is the most critical issue
Probabilities of Normal Distribution
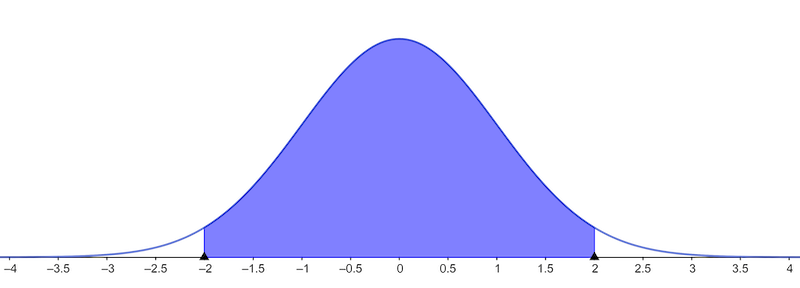
≈95% of normal population is between \(-2\cdot\text{sd}(\mathbf x)\) and \(2\cdot\text{sd}(\mathbf x)\)
≈99% of normal population is between \(-3\cdot\text{sd}(\mathbf x)\) and \(3\cdot\text{sd}(\mathbf x)\)