Class 6: Statistical uncertainty
Methodology of Scientific Research
Andrés Aravena, PhD
March 24, 2022
Measuring
What is a measurement?
- A measurement tells us about a property of something
- It gives a number to that property
- Measurements are always made using an instrument of some kind
- Rulers, stopwatches, weighing scales, thermometers, etc.
- The result of a measurement has two parts: a number and a unit of measurement
Measurement Good Practice Guide No. 11 (Issue 2). A Beginner’s Guide to Uncertainty of Measurement. Stephanie Bell. Centre for Basic, Thermal and Length Metrology National Physical Laboratory. UK
What is not a measurement?
There are some processes that might seem to be measurements, but are not. For example
- Counting is not normally viewed as a measurement
- Tests that lead to a ‘yes/no’ answer or a ‘pass/fail’ result
- Comparing two pieces of string to see which one is longer
However, measurements may be part of the process of a test
Measurements have uncertainty
Uncertainty of measurement is the doubt about the result of a measurement, due to
- resolution
- random errors
- systematic errors
Observational error
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results
Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case
Random error which may vary from observation to another
Error versus uncertainty
Do not to confuse error and uncertainty
Error is the difference between the measured and the “true” value
Uncertainty is a quantification of the doubt about the result
Whenever possible we try to correct for any known errors
But any error whose value we do not know is a source of uncertainty
Where do errors and uncertainties come from?
Flaws in the measurement can come from:
The measuring instrument – instruments can suffer from errors including wear, drift, poor readability, noise, etc.
The item being measured – which may not be stable (measure the size of an ice cube in a warm room)
The measurement process – the measurement itself may be difficult to make. Measuring the weight of small animals presents particular difficulties
‘Imported’ uncertainties – calibration of your instrument has an uncertainty
Where do errors and uncertainties come from?
Operator skill – One person may be better than another at reading fine detail by eye. The use of an a stopwatch depends on the reaction time of the operator
Sampling issues – the measurements you make must be representative. If you are choosing samples from a production line, don’t always take the first ten made on a Monday morning
The environment – temperature, air pressure, humidity and many other conditions can affect the measuring instrument or the item being measured
Reading v/s measurement
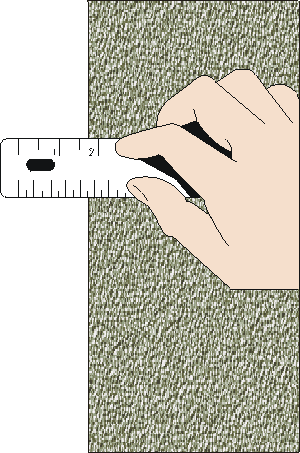
A reading is one observation of the instrument
A measurement may require several reads
For example, to measure a length, we make two reads, and we calculate the difference
The measurement will accumulate the uncertainty
Precise ≠ Accurate
Precision, accuracy, and trueness
In this context, people has defined the following ideas
- accuracy: closeness of measurements to the true value
- precision: closeness of the measurements to each other
- trueness: closeness of the mean of a set of measurement to the true value
BS ISO 5725-1: “Accuracy (trueness and precision) of measurement methods and results - Part 1: General principles and definitions.”, p.1 (1994)
Precision v/s trueness
High trueness, Low precision
High precision, Low trueness
In a graphic
Historical note
In some old material, people say “accuracy” in place of trueness
Other people say bias
These words are still common in science and technology
Be aware of this discrepancy
Uncertainty
Knowing the uncertainty

Uncertainty of a single read
For a single read, the uncertainty depends at least on the instrument resolution
For example, my water heater shows temperature with 5°C resolution: 50, 55, 60,…
If it shows 55°C, the real temperature is somewhere between 53°C and 57°C
We write 55°C ± 2.5°C
For a single read, \(Δx\) is half of the resolution
The easy rule
Last class we saw the easy rule for error propagation
\[ \begin{aligned} (x ± Δx) + (y ± Δy) & = (x+y) ± (Δx+Δy)\\ (x ± Δx) - (y ± Δy) & = (x-y) ± (Δx+Δy)\\ (x ± Δx\%) \times (y ± Δy\%)& =xy ± (Δx\% + Δy\%)\\ (x ± Δx\%) ÷ (y ± Δy\%)& =x/y ± (Δx\% + Δy\%) \end{aligned} \]
Here \(Δx\%\) represents the relative uncertainty, that is \(Δx/x\)
We use absolute uncertainty for + and -, and relative uncertainty for ⨉ and ÷
Be careful whit absolute and relative
It is easy to get confused with relative errors
Instead of \((x ± Δx\%)\) it is better to write \[x(1± Δx/x)\]
Mathematical notation was invented to make things clear, not confusing
Exercise
Let’s verify the formulas of the previous slide
Remember that we assume that \(Δx/x\) is small
General formula for a function
Assuming that the errors are small compared to the main value, we can find the error for any “reasonable” function
For any smooth function \(f,\) we have \[f(x±Δx) = f(x) ± \frac{df}{dx}(x)\cdot Δx + \frac{d^2f}{dx^2}(x+\varepsilon)\cdot \frac{Δx^2}{2}\] When \(Δx\) is small, we can ignore the last part, so
Mean value theorem
If \(f\) is smooth, there is a value \(c\) between \(a\) and \(b\) such that \[\frac{f(b)-f(a)}{b-a}=\frac{df}{dx}(c)\]
Exercises
\[(x±Δx)^2\] \[\ln(x±Δx)\] \[\log_{10}(x)\] \[\exp(x±Δx)\]
qPCR
qPCR depends on initial concentration
The curve depends on the initial DNA concentration
Finding the initial concentration
We care only about the exponential phase
The signal increases 2 times on every cycle
\[X(C) = X(0)⋅2^C\]
So we can find the initial concentration
\[X(0) = X(C)⋅2^{-C}\]
CT: cycle where Signal crosses threshold
DNA concentration crosses 50% at 13.73 cycles
Different threshold
DNA concentration crosses 5% at 10 cycles
Standard curve: CT changes with concentration
Start with a large concentration of template, and dilute it several times. Measure the CT of each dilution
Errors may compensate
Probabilistic uncertainty propagation
These rules are “pessimistic”. They give the worst case
In general the “errors” can be positive or negative, and they tend to compensate
(This is valid only if the errors are independent)
In this case we can analyze uncertainty using the rules of probabilities
Variance quantifies uncertainty
In this case, the value \(Δx\) will represent the standard deviation of the measurement
The standard deviation is the square root of the variance
Then, we combine variances using the rule
“The variance of a sum is the sum of the variances”
(Again, this is valid only if the errors are independent)
The probabilistic rule
\[ \begin{align} (x ± Δx) + (y ± Δy) & = (x+y) ± \sqrt{Δx^2+Δy^2}\\ (x ± Δx) - (y ± Δy) & = (x-y) ± \sqrt{Δx^2+Δy^2}\\ (x ± Δx\%) \times (y ± Δy\%)& =x y ± \sqrt{Δx\%^2+Δy\%^2}\\ \frac{x ± Δx\%}{y ± Δy\%} & =\frac{x}{y} ± \sqrt{Δx\%^2+Δy\%^2} \end{align} \]
Confidence interval for the measurement
When using probabilistic rules we need to multiply the standard deviation by a constant k, associated with the confidence level
In most cases (but not all), the uncertainty follows a Normal distribution. In that case
- \(k=1.96\) corresponds to 95% confidence
- \(k=2.00\) corresponds to 98.9% confidence
- \(k=2.57\) corresponds to 99% confidence
- \(k=3.00\) corresponds to 99.9% confidence
Not all uncertainties are alike
Previously we considered one kind of uncertainty: the instrument resolution
This is a “one time” error
- We notice it immediately
- It does not change if we measure again
Two ways to estimate uncertainties
- Type A - uncertainty estimates using statistics
- (usually from repeated readings)
- Type B - uncertainty estimates from any other
information.
- past experience of the measurements, calibration certificates, manufacturer’s specifications, calculations, published information, common sense
In most measurement situations, uncertainty evaluations of both types are needed
Measurement Good Practice Guide No. 11 (Issue 2). A Beginner’s Guide
to Uncertainty of Measurement.
Stephanie Bell. Centre for Basic, Thermal and Length Metrology National
Physical Laboratory. UK
Standard deviation of discretization
Standard deviation of rectangular distribution is \[u=\frac{a}{\sqrt{3}}\] when the width of the rectangle is \(2a\)
Standard deviation of thermal noise
Standard deviation of noise can be estimated from the data: \[s=\sqrt{\frac{1}{n-1}\sum_i (x_i - \bar x)^2}\]
Standard deviation of average
If the measures are random, their average is also random
It has the same mean but less variance
Standard error of the average of samples is \[\frac{s}{\sqrt{n}}\]


.svg)