Class 6: Global and Local Alignment
Bioinformatics
Andrés Aravena
October 14, 2021
There is a better way to find the best
We will see more details later
The idea is to draw a rectangle
- One sequence in the rows
- Another sequence in the columns
- Mark the cells where row letter and column letter are equal
It looks like this

The goal is to move from one corner to the other
Jumping black to black is free
Horizontal and vertical moves are gaps
We move from one corner to the other

White blocks add to the distance

Comparing a sequence with itself

Comparing a sequence with itself
 This allow us to find repeats inside the sequence
This allow us to find repeats inside the sequence
Palindromic sequences / Hairpins
 A sequence is said palindromic when it repeats itself backwards
A sequence is said palindromic when it repeats itself backwards
In RNA that results in a single-strand structure called hairpin
They are usually transcription terminators
Exercise
Prepare a DotPlot in Excel or Google Sheets
Partial matching
Levenstein distance is Global Alignment
Useful to compare proteins
But not good when we look for a gene in a genome
or a domain in a protein
What shall we do when the query is much smaller than all subjects?
Semi-global alignment

In this case we want to go from one side to the other
Gaps in semi-global alignment
The query is much smaller than the subject
In this case we distinguish two kind of gaps
Internal gaps, inside the sequences
External gaps, outside the query sequence
External gaps do not count
External gaps are caused by the experiment
For example, we use PCR to cut part of a genome
Therefore anything outside the sequence cannot be seen for technical reasons
Internal gaps do count
Internal gaps are caused by nature
They are gained or lost during replication
They have biological meaning
Therefore, they must be counted
We showed Edit distance
“Distance” means that smaller numbers are better
If the distance is 0, then the two sequences are identical
If the distance is small, the two sequences are similar
If the distance is big, the sequences are different
Different alignments for different questions
- Global alignment compares genes to genes, or proteins to proteins
- We expect that both sequences are similar
- Semi-global alignment compares genes to genomes
- We expect that query is similar to part of subject
- Local alignment compares genomes to genomes
- We expect that part of the query is similar to part of subject
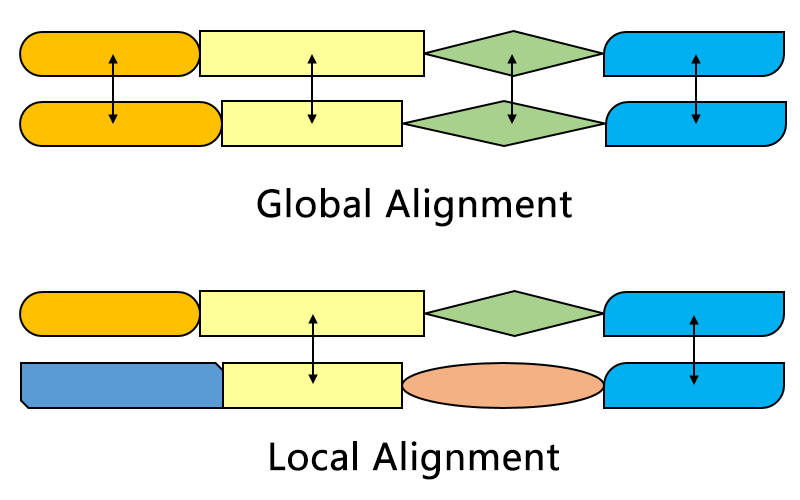
Global alignment
- all sequences must match.
- Each gap is penalized
Semi-global alignment
- all sequences must match, but one may be shorter than the other.
- external gaps are not penalized
Local alignment
- Some part of the sequence must match
- external gaps are not penalized
- can be with or without internal gaps
Global v/s local
Part of query to part of subject
ABRACADABRA
CHUPACABRAExternal gaps do not count
ABRACADABRA
||||
CHUPACABRALocal alignment is not a distance
Since external gaps do not count, we can always use them
In this case the smallest distance is always 0
The smallest cost is achieved taking one letter
ABRACADABRA
|
CHUPACABRAWe cannot solve the minimization problem
Score instead of distance
Instead of finding a minimum, we look for a maximum
- Matching places get positive score
- Mismatch and gaps get negative score
The philosophy is the same, but we look for big numbers instead of small numbers
The Optimal Alignment is the one with largest score
Dot plot becomes a matrix
Initially we placed 1 or 0 on each cell depending on match or mismatch
Now we put positive or negative numbers, depending of single-letter scores
Substitution scoring matrices
Single-letter scores (example)
If we pair two letters \(x\) and \(y\), we need to know how they contribute to the score value. For example,
- If \(x = y\) the score increases by 1
- If \(x ≠ y\) the score decreases by 1
- If one of the letters is
-(a gap), the score reduces by 2
In general, we have a substitution scoring matrix \(C_{x, y}\) for each \(x\) and \(y\)
Single-letter scores (example)
In one equation
\[C_{x, y} = \begin{cases} +1 & \quad x=y\\ -1 & \quad x≠y\\ -2 & \quad x=\texttt{"-"} \\ -2 & \quad y=\texttt{"-"} \end{cases}\]
Substitution Scoring matrices
The Substitution Scoring Matrix has one row and one column for each letter in our alphabet
For example 4 rows and 4 columns for DNA sequences
In DNA it is common to have +1 for match and -2 for mismatch
Sometimes we can use (+1,-3), (+1,-1) or even (4,-5)
DNA scoring matrix
A C G T
A 1 -2 -2 -2
C -2 1 -2 -2
G -2 -2 1 -2
T -2 -2 -2 1Amino-acid scoring matrices
For proteins the alphabet has 20 letters, so the scoring matrix is 20×20
The scores of these matrices are based on the relative frequency of each mutation in nature
Obviously, we only care about non-lethal mutations
More specifically, we care about the Point Mutations that are Accepted
These are called PAM matrices (Margaret Dayhoff, 1978)
PAM matrices
Based on 1572 mutations in 71 families of closely related proteins
Dayhoff only used alignments having at least 85% identity
She assumed that any aligned mismatches were the result of a single mutation event, rather than several at the same location
PAM matrices
PAM1 is the scoring matrix for proteins in a “short” period
With some easy mathematics we can calculate PAM2, PAM30, PAM250, etc
They represent mutations in 2, 30, and 250 short periods
PAM30 matrix
A R N D C Q E G H I L K M F P S T W Y V B J Z X *
A 6 -7 -4 -3 -6 -4 -2 -2 -7 -5 -6 -7 -5 -8 -2 0 -1 -13 -8 -2 -3 -6 -3 -1 -17
R -7 8 -6 -10 -8 -2 -9 -9 -2 -5 -8 0 -4 -9 -4 -3 -6 -2 -10 -8 -7 -7 -4 -1 -17
N -4 -6 8 2 -11 -3 -2 -3 0 -5 -7 -1 -9 -9 -6 0 -2 -8 -4 -8 6 -6 -3 -1 -17
D -3 -10 2 8 -14 -2 2 -3 -4 -7 -12 -4 -11 -15 -8 -4 -5 -15 -11 -8 6 -10 1 -1 -17
C -6 -8 -11 -14 10 -14 -14 -9 -7 -6 -15 -14 -13 -13 -8 -3 -8 -15 -4 -6 -12 -9 -14 -1 -17
Q -4 -2 -3 -2 -14 8 1 -7 1 -8 -5 -3 -4 -13 -3 -5 -5 -13 -12 -7 -3 -5 6 -1 -17
E -2 -9 -2 2 -14 1 8 -4 -5 -5 -9 -4 -7 -14 -5 -4 -6 -17 -8 -6 1 -7 6 -1 -17
G -2 -9 -3 -3 -9 -7 -4 6 -9 -11 -10 -7 -8 -9 -6 -2 -6 -15 -14 -5 -3 -10 -5 -1 -17
H -7 -2 0 -4 -7 1 -5 -9 9 -9 -6 -6 -10 -6 -4 -6 -7 -7 -3 -6 -1 -7 -1 -1 -17
I -5 -5 -5 -7 -6 -8 -5 -11 -9 8 -1 -6 -1 -2 -8 -7 -2 -14 -6 2 -6 5 -6 -1 -17
L -6 -8 -7 -12 -15 -5 -9 -10 -6 -1 7 -8 1 -3 -7 -8 -7 -6 -7 -2 -9 6 -7 -1 -17
K -7 0 -1 -4 -14 -3 -4 -7 -6 -6 -8 7 -2 -14 -6 -4 -3 -12 -9 -9 -2 -7 -4 -1 -17
M -5 -4 -9 -11 -13 -4 -7 -8 -10 -1 1 -2 11 -4 -8 -5 -4 -13 -11 -1 -10 0 -5 -1 -17
F -8 -9 -9 -15 -13 -13 -14 -9 -6 -2 -3 -14 -4 9 -10 -6 -9 -4 2 -8 -10 -2 -13 -1 -17
P -2 -4 -6 -8 -8 -3 -5 -6 -4 -8 -7 -6 -8 -10 8 -2 -4 -14 -13 -6 -7 -7 -4 -1 -17
S 0 -3 0 -4 -3 -5 -4 -2 -6 -7 -8 -4 -5 -6 -2 6 0 -5 -7 -6 -1 -8 -5 -1 -17
T -1 -6 -2 -5 -8 -5 -6 -6 -7 -2 -7 -3 -4 -9 -4 0 7 -13 -6 -3 -3 -5 -6 -1 -17
W -13 -2 -8 -15 -15 -13 -17 -15 -7 -14 -6 -12 -13 -4 -14 -5 -13 13 -5 -15 -10 -7 -14 -1 -17
Y -8 -10 -4 -11 -4 -12 -8 -14 -3 -6 -7 -9 -11 2 -13 -7 -6 -5 10 -7 -6 -7 -9 -1 -17
V -2 -8 -8 -8 -6 -7 -6 -5 -6 2 -2 -9 -1 -8 -6 -6 -3 -15 -7 7 -8 0 -6 -1 -17
B -3 -7 6 6 -12 -3 1 -3 -1 -6 -9 -2 -10 -10 -7 -1 -3 -10 -6 -8 6 -8 0 -1 -17
J -6 -7 -6 -10 -9 -5 -7 -10 -7 5 6 -7 0 -2 -7 -8 -5 -7 -7 0 -8 6 -6 -1 -17
Z -3 -4 -3 1 -14 6 6 -5 -1 -6 -7 -4 -5 -13 -4 -5 -6 -14 -9 -6 0 -6 6 -1 -17
X -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -17
* -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 1BLOSUM matrices
Using local alignment we can identify conserved regions
In 1992 Steven Henikoff and Jorja Henikoff created new substitution matrices based on local alignment of blocks
BLOcks SUbstitution Matrix
Idea: each protein domain can evolve at different speeds
BLOSUM62
A R N D C Q E G H I L K M F P S T W Y V B J Z X *
A 4 -1 -2 -2 0 -1 -1 0 -2 -1 -1 -1 -1 -2 -1 1 0 -3 -2 0 -2 -1 -1 -1 -4
R -1 5 0 -2 -3 1 0 -2 0 -3 -2 2 -1 -3 -2 -1 -1 -3 -2 -3 -1 -2 0 -1 -4
N -2 0 6 1 -3 0 0 0 1 -3 -3 0 -2 -3 -2 1 0 -4 -2 -3 4 -3 0 -1 -4
D -2 -2 1 6 -3 0 2 -1 -1 -3 -4 -1 -3 -3 -1 0 -1 -4 -3 -3 4 -3 1 -1 -4
C 0 -3 -3 -3 9 -3 -4 -3 -3 -1 -1 -3 -1 -2 -3 -1 -1 -2 -2 -1 -3 -1 -3 -1 -4
Q -1 1 0 0 -3 5 2 -2 0 -3 -2 1 0 -3 -1 0 -1 -2 -1 -2 0 -2 4 -1 -4
E -1 0 0 2 -4 2 5 -2 0 -3 -3 1 -2 -3 -1 0 -1 -3 -2 -2 1 -3 4 -1 -4
G 0 -2 0 -1 -3 -2 -2 6 -2 -4 -4 -2 -3 -3 -2 0 -2 -2 -3 -3 -1 -4 -2 -1 -4
H -2 0 1 -1 -3 0 0 -2 8 -3 -3 -1 -2 -1 -2 -1 -2 -2 2 -3 0 -3 0 -1 -4
I -1 -3 -3 -3 -1 -3 -3 -4 -3 4 2 -3 1 0 -3 -2 -1 -3 -1 3 -3 3 -3 -1 -4
L -1 -2 -3 -4 -1 -2 -3 -4 -3 2 4 -2 2 0 -3 -2 -1 -2 -1 1 -4 3 -3 -1 -4
K -1 2 0 -1 -3 1 1 -2 -1 -3 -2 5 -1 -3 -1 0 -1 -3 -2 -2 0 -3 1 -1 -4
M -1 -1 -2 -3 -1 0 -2 -3 -2 1 2 -1 5 0 -2 -1 -1 -1 -1 1 -3 2 -1 -1 -4
F -2 -3 -3 -3 -2 -3 -3 -3 -1 0 0 -3 0 6 -4 -2 -2 1 3 -1 -3 0 -3 -1 -4
P -1 -2 -2 -1 -3 -1 -1 -2 -2 -3 -3 -1 -2 -4 7 -1 -1 -4 -3 -2 -2 -3 -1 -1 -4
S 1 -1 1 0 -1 0 0 0 -1 -2 -2 0 -1 -2 -1 4 1 -3 -2 -2 0 -2 0 -1 -4
T 0 -1 0 -1 -1 -1 -1 -2 -2 -1 -1 -1 -1 -2 -1 1 5 -2 -2 0 -1 -1 -1 -1 -4
W -3 -3 -4 -4 -2 -2 -3 -2 -2 -3 -2 -3 -1 1 -4 -3 -2 11 2 -3 -4 -2 -2 -1 -4
Y -2 -2 -2 -3 -2 -1 -2 -3 2 -1 -1 -2 -1 3 -3 -2 -2 2 7 -1 -3 -1 -2 -1 -4
V 0 -3 -3 -3 -1 -2 -2 -3 -3 3 1 -2 1 -1 -2 -2 0 -3 -1 4 -3 2 -2 -1 -4
B -2 -1 4 4 -3 0 1 -1 0 -3 -4 0 -3 -3 -2 0 -1 -4 -3 -3 4 -3 0 -1 -4
J -1 -2 -3 -3 -1 -2 -3 -4 -3 3 3 -3 2 0 -3 -2 -1 -2 -1 2 -3 3 -3 -1 -4
Z -1 0 0 1 -3 4 4 -2 0 -3 -3 1 -1 -3 -1 0 -1 -2 -2 -2 0 -3 4 -1 -4
X -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -4
* -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 1