1. Rabbits

⊕ Figure 1. Leonardo Fibonacci, expert on rabbits and numbers.

Near 1170, in the Italian city of Pisa, the son of Guglielmo Bonacci was born. He was named Leonardo. Nowadays, he is known as Leonardo Pisano (meaning “Leonardo of Pisa”) and also as Leonardo Fibonacci (short for “filius Bonacci”, that is, “son of Bonacci”).

Leonardo traveled with his father and, while staying in the city of Béjaïa (Algeria), he was sent to study calculation with an Arab master. He later went to Egypt, Syria, Greece, Sicily, and Provence, where he studied different numerical systems and methods of calculation. He soon realized the many advantages of the Hindu-Arabic system, as introduced first by the famous mathematician Muḥammad ibn Mūsā al-Khwārizmī (born c. 780—died c. 850 in Baghdad).

In 1202, Leonardo wrote the “Book of Calculation” which helped europeans to learn the Hindu–Arabic numerals. In that book he wrote:

A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?

He made the following simplifying assumptions about the population:

• The population begins in the first month with a pair of newborn rabbits.
• Rabbits reach reproductive age after one month.
• In any given month, every rabbit of reproductive age mates with another rabbit of reproductive age.
• Exactly one month after two rabbits mate, they produce one male and one female rabbit.
• Rabbits never die or stop reproducing.

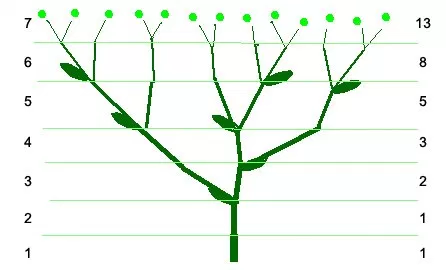⊕ Figure 2. Fibonacci numbers are often found in nature.

Fibonacci’s exercise was to calculate how many pairs of rabbits would remain in one year. We can see that in the second month, the first pair of rabbits reach reproductive age and mate. In the third month, another pair of rabbits is born, and we have two rabbit pairs; our first pair of rabbits mates again. In the fourth month, another pair of rabbits is born to the original pair, while the second pair reach maturity and mate (with three total pairs). After a year, the rabbit population has 144 pairs.

Beyond rabbits, it has been observed that Fibonacci numbers appear often in nature; for example, in the spirals of sunflower heads, in pine cones, in the genealogy of the male bee, in the spiral in snail shells, in the arrangement of leaf buds on a stem, and in animal horns. You can see some of them looking for “Fibonacci in nature” on Google images.

Doing some abstraction, we can use fib(n) to represent the number of pairs of rabbits on month n. The numbers have the following rules:

• fib(0) = 0
• fib(1) = 1
• fib(n) = fib(n-1) + fib(n-2)

Your task is to write a recursive function in R that has input n and output fib(n). Remember that recursive means that the function calls itself, like in the factorial example. You can test your function by checking that at the end of the first year there are 144 pairs of rabbits.

⊕ Figure 3. You should see something like this.

2. Draw heads, hands and legs

As we discussed in class, advanced software engineering uses stick-people to model actors in “use case scenarios”. You can learn more looking for Universal Modeling Language. We want to draw one or more stick-people with the following function

⊕ Figure 4. You can also draw something like this.

draw_person <- function(size) {
    draw_head(size*1.2)
    turtle_left(180)
    turtle_forward(size)
    turtle_left(90)
    draw_arm(size*1.5)
    turtle_left(180)
    draw_arm(size*1.5)
    turtle_left(90)
    turtle_forward(size*2)
    turtle_left(20)
    draw_leg(size*2)
    turtle_right(40)
    draw_leg(size*2)
}

Your task is to write the functions draw_head(), draw_arm() and draw_leg(). They should look like Figure 3, but you can make creative modifications, like hands with fingers, hair, etc.

The most important issue is that each of your functions must leave the turtle in the same position and the same angle as before. Your function can move the turtle as you wish, but it must leave the turtle as it was at the beginning of the function.

Hint: You are free to use any command although you only need turtle_left(), turtle_right(), turtle_forward() and turtle_backward(). Nothing else is required.

⊕ Figure 5. Examples of Trees.

3. Trees and branches

Another recursive structure found in nature are trees. Each branch is like a small tree. More precisely, a tree with n levels has branches with n-1 levels. Your task is to make a function to draw trees with three branches.

If you want to be sure of understanding the English names of the parts of a tree you can check this figure.

The function should be named tree() with three inputs: the number of levels n, the length of the trunk length, and the angle between the branches angle. Each branch is a tree with n-1 levels and with length equal to 0.8 times the length of the previous level. The first branch of every tree is angle degrees to the left of the trunk; the second is aligned with the trunk, and the last one is angle degrees to the right of the trunk.

Like in the previous exercise, the most important issue is that the tree() functions must leave the turtle in the same position and the same angle as before. Your function can move the turtle as you wish, but it must leave the turtle as it was at the beginning of the function.

You can test your function with the commands tree(6, 23, 25), tree(4, 15, 15), and tree(7, 8, 38). Each command should produce something like Figure 5.

Extra points: Modify the tree() function to make the width of each branch part equal to the level. Can you change the color of each part, like in this example?

Delivery

Please send me the quiz2.R file in a single email to andres.aravena+cmb@istanbul.edu.tr. Do not forget to write your name and number.