1. Replicate plots from last class

In the last class we simulated the water formation system under different rates and initial conditions. The system is represented by this graph:

The code to make one simulation is this:

water_formation <- function(N, r1_rate,  r2_rate, H_ini, O_ini, W_ini) {
  W <- d_W <- rep(NA, N) # Water, quantity and change on each time
  H <- d_H <- rep(NA, N) # Hydrogen
  O <- d_O <- rep(NA, N) # Oxygen
  W[1] <- W_ini
  H[1] <- H_ini
  O[1] <- O_ini
  d_W[1] <- d_H[1] <- d_O[1] <- 0 # the initial change is zero

  for(i in 2:N) {
    d_W[i] <-    r1_rate*H[i-1]*H[i-1]*O[i-1] - r2_rate*W[i-1]
    d_O[i] <-   -r1_rate*H[i-1]*H[i-1]*O[i-1] + r2_rate*W[i-1]
    d_H[i] <- -2*r1_rate*H[i-1]*H[i-1]*O[i-1] + 2*r2_rate*W[i-1]

    W[i] <- W[i-1] + d_W[i]
    O[i] <- O[i-1] + d_O[i]
    H[i] <- H[i-1] + d_H[i]
  }
  return(data.frame(Step=1:N, W, H, O))
}

Please write the code to draw the following plot. You will need to simulate several times for different rates and initial conditions

2. Simulate a chaotic system

In the class we also saw a chaotic system, that can have high sensitivity to initial conditions. The system is very simple

After simplification, this system can be simulated by the following code:

quad_map <- function(N, A, x_ini) {
  x <- rep(NA, N)
  x[1] <- x_ini
  for(i in 2:N) {
    x[i] <- A * x[i-1] * (1 - x[i-1])
  }
  return(x)
}

As we said, the behavior depends on the value of A. Please write the code that simulates this system for different values of A from 2.9 to 4 by 0.001, with x_ini=0.4 and N=1500. Take the final 500 values of each simulation and draw them using pch=".". You should see this:

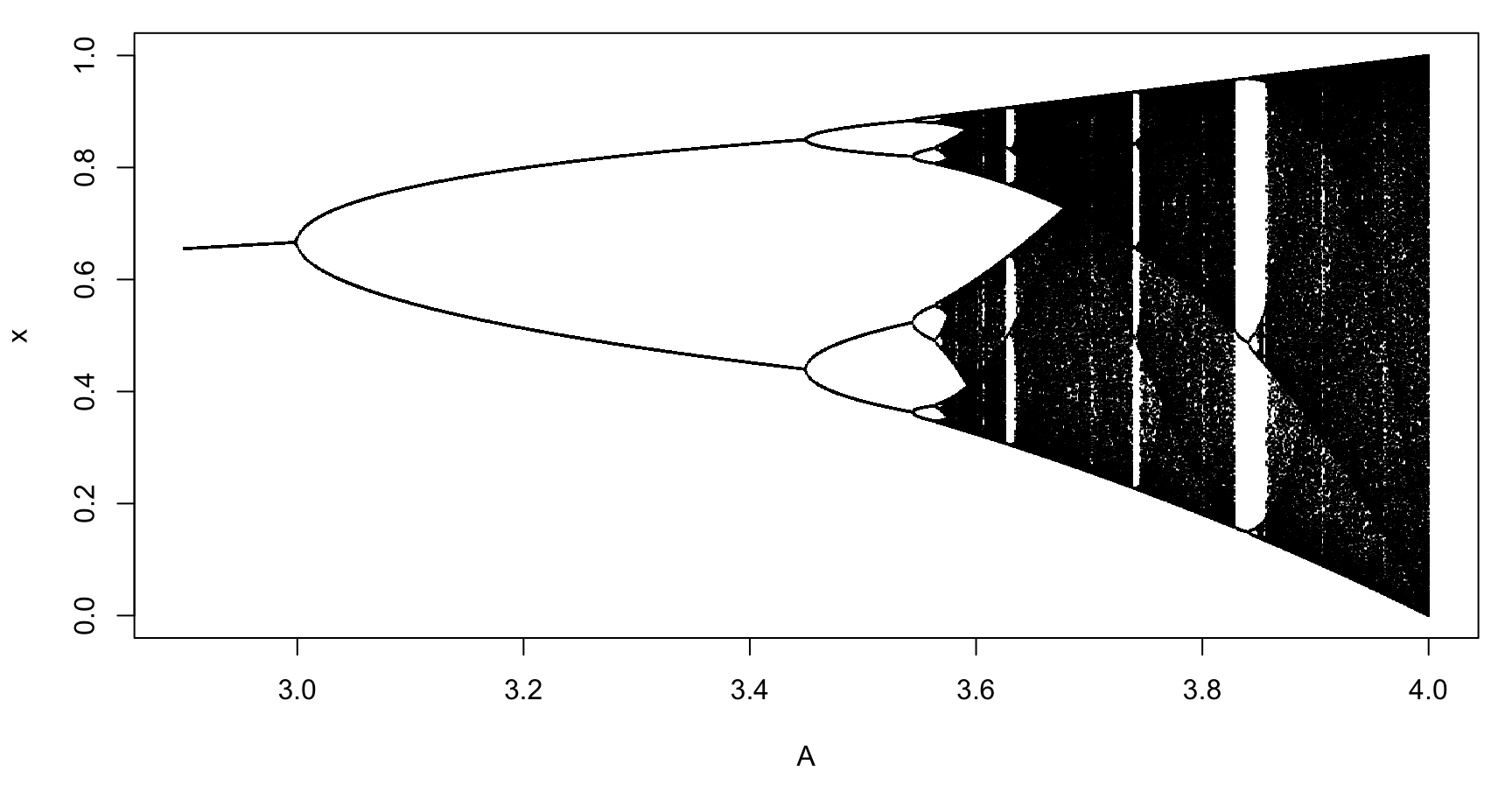
There are at least two ways to do this plot.

• Make a very long vector with 500 values from each simulation, and plot all in one command
• Draw first an empty plot using type="n", and then use the function points() to add the 500 values of each simulation separately

3. Many dice

In class we simulated throwing two dice at the same time. What if we throw 3 dice? Or 10? Or 100?

Please write the code to simulate N times the experiment “throw M dice and count the total of points”. Something like

many_dice <- function(N, M) {
    # repeat N times
        # throw M dice
        # sum them
        # put the result in a vector `ans`
    # return `ans` vector
}

If you do it right, you should be able to draw a plot like this: