Class 8: Statistical uncertainty
Methodology of Scientific Research
Andrés Aravena, PhD
March 14, 2024
Measuring
What is a measurement?
A measurement tells us about a property of something
- It gives a number to that property
Measurements are always made using an instrument
- Rulers, stopwatches, scales, thermometers, etc.
The result of a measurement has two parts:
- A number and a unit of measurement
Measurement Good Practice Guide No. 11 (Issue 2).
A Beginner’s Guide to Uncertainty of Measurement. Stephanie Bell.
Centre for Basic, Thermal and Length Metrology National Physical
Laboratory. UK
What is not a measurement?
There are some processes that might seem to be measurements, but are not. For example
- Counting is not normally viewed as a measurement
- Tests that lead to a ‘yes/no’ answer or a ‘pass/fail’ result
- Comparing two pieces of string to see which one is longer
However, measurements may be part of the process of a test
Measurements have uncertainty
Uncertainty of measurement is the doubt about the result of a measurement, due to
- resolution
- random errors
- systematic errors
Uncertainty must be declared
How big is the margin? How bad is the doubt?
We declare an interval: \([x_\text{min}, x_\text{max}]\)
Most of the time we write x ± 𝚫x
Example: 20cm ± 1cm
Error versus uncertainty
Do not to confuse error and uncertainty
Error is the difference between the measured and the “true” value
Uncertainty is a quantification of the doubt about the result
Whenever possible we try to correct for any known errors
But any error whose value we do not know is a source of uncertainty
Where do errors and uncertainties come from?
Flaws in the measurement can come from
The measuring instrument
The item being measured
The measurement process
‘Imported’ uncertainties
Operator skill
Sampling issues
The environment
The measuring instrument
instruments can suffer from errors including
wear,
drift,
poor readability,
noise,
etc.
The item being measured
The thing we measure may not be stable
For example, when we measure the size of an ice cube in a warm room
The measurement process
The measurement itself may be difficult to make
Measuring the weight of small animals presents particular difficulties
‘Imported’ uncertainties
Calibration of your instrument has an uncertainty
Operator skill
One person may be better than another at reading fine detail by eye
The use of an a stopwatch depends on the reaction time of the operator
Sampling issues
The measurements you make must be representative
If you are choosing samples from a production line, don’t always take the first ten made on a Monday morning
The environment
Temperature
Air pressure
Humidity
and many other conditions can affect the measuring instrument or the item being measured
Observational error
Reading v/s measurement
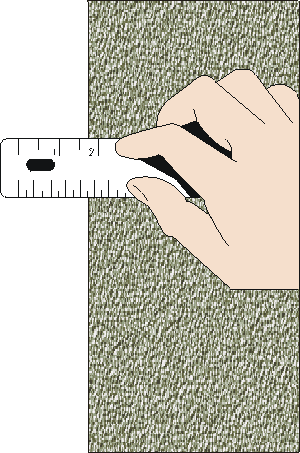
A reading is one observation of the instrument
A measurement may require several reads
For example, to measure a length, we make two reads, and we calculate the difference
The measurement will accumulate the uncertainty
Uncertainty of a single read
For a single read, the uncertainty depends at least on the instrument resolution
For example, my old water heater showed temperature with 5°C resolution: 50, 55, 60,…

Real vs measured value
If it shows 55°C, the real temperature is somewhere between 53°C and 57°C
We write 55°C ± 2.5°C
For a single read, 𝚫x = half of the resolution
This is a “one time” error
- We notice it immediately
- It does not change if we measure again
Two kinds of observational error
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results
Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case
Random error which may vary from observation to another
Two ways to estimate uncertainties
Type A - uncertainty estimates using statistics
- (usually from repeated readings)
Type B - uncertainty estimates from any other information.
- past experience of the measurements, calibration certificates, manufacturer’s specifications, calculations, published information, common sense
In most measurement situations, uncertainty evaluations of both types are needed
Measurement Good Practice Guide No. 11 (Issue 2). A Beginner’s Guide
to Uncertainty of Measurement.
Stephanie Bell. Centre for Basic, Thermal and Length Metrology National
Physical Laboratory. UK
Discretization uncertainty
My old water heater
My new water heater
Distribution of discretization error
More samples give higher precision, but not better accuracy
Noise
There are other sources of uncertainty: noise
When the instrument resolution is good, we observe that the measured values change on every read
In many cases this is due to thermal effects, or other sources of noise
Example
Distribution of thermal noise
Usually the variability follows a Normal distribution
Real v/s measured data
This would be the case when resolution is very high
Combined uncertainty
Combining Uncertainty
Sum of two measurements:
\[(x ± 𝚫x) + (y ± 𝚫y) = (x+y) ±
(𝚫x+𝚫y)\]
Difference between measurements:
\[(x ± 𝚫x) - (y ± 𝚫y) = (x-y) ±
(𝚫x+𝚫y)\]
Multiplying Uncertainty
To calculate \((x ± 𝚫x) × (y ± 𝚫y)\) we first write the uncertainty as percentage
\[(x ± 𝚫x/x\%) × (y ± 𝚫y/y\%)\]
Then we sum the percentages:
\[xy ± (𝚫x/x + 𝚫y/y)\%\]
Finally we convert back to the original units:
\[xy ± xy(𝚫x/x + 𝚫y/y)\]
General formula
Assuming that the errors are small compared to the main value, we can find the error for any “reasonable” function
Taylor’s Theorem says that, for any derivable function \(f,\) we have
\[ f(x±𝚫x) = f(x) ± \frac{df}{dx}(x)\cdot 𝚫x + \frac{d^2f}{dx^2}(x+\varepsilon)\cdot \frac{𝚫x^2}{2} \]
When \(𝚫x\) is small, we can ignore the last part.
Example 1
\[ \begin{aligned} (x ±𝚫x)^2& ≈ x^2 ± 2x\cdot𝚫x\\ & = x^2 ± 2x^2\cdot\frac{𝚫x}{x} \\ & = x^2 ± 2𝚫x\% \end{aligned} \]
because \[\frac{dx^2}{dx}=2x\]
Example 2
\[ \begin{align} \sqrt{x ±𝚫x}& ≈ \sqrt x ± \frac{1}{2\sqrt x}\cdot 𝚫x\\ & = \sqrt x ± \frac{1}{2}\sqrt x\cdot \frac{𝚫x}{x}\\ & = \sqrt x ± \frac{1}{2}𝚫x\% \end{align} \]
because \[\frac{d\sqrt x}{dx}=\frac 1 {2\sqrt x}\]
Errors may compensate
Probabilistic uncertainty propagation
These rules are “pessimistic”. They give the worst case
In general the “errors” can be positive or negative, and they tend to compensate
(This is valid only if the errors are independent)
In this case we can analyze uncertainty using the rules of probabilities
Variance quantifies uncertainty
In this case, the value \(Δx\) will represent the standard deviation of the measurement
The standard deviation is the square root of the variance
Then, we combine variances using the rule
“The variance of a sum is the sum of the variances”
(Again, this is valid only if the errors are independent)
The probabilistic rule
\[ \begin{align} (x ± Δx) + (y ± Δy) & = (x+y) ± \sqrt{Δx^2+Δy^2}\\ (x ± Δx) - (y ± Δy) & = (x-y) ± \sqrt{Δx^2+Δy^2}\\ (x ± Δx\%) \times (y ± Δy\%)& =x y ± \sqrt{Δx\%^2+Δy\%^2}\\ \frac{x ± Δx\%}{y ± Δy\%} & =\frac{x}{y} ± \sqrt{Δx\%^2+Δy\%^2} \end{align} \]
Confidence interval for the measurement
When using probabilistic rules we need to multiply the standard deviation by a constant k, associated with the confidence level
In most cases (but not all), the uncertainty follows a Normal distribution. In that case
- \(k=1.96\) corresponds to 95% confidence
- \(k=2.00\) corresponds to 98.9% confidence
- \(k=2.57\) corresponds to 99% confidence
- \(k=3.00\) corresponds to 99.9% confidence
Standard deviation of thermal noise
Standard deviation of noise can be estimated from the data: \[s=\sqrt{\frac{1}{n-1}\sum_i (x_i - \bar x)^2}\]
Standard deviation of average
If the measures are random, their average is also random
It has the same mean but less variance
Standard error of the average of samples is \[\frac{s}{\sqrt{n}}\]
Standard deviation of discretization
Standard deviation of rectangular distribution is \[u=\frac{a}{\sqrt{3}}\] when the width of the rectangle is \(2a\)
How to combine
The exact distribution is hard to calculate
International standards suggest using computer simulation
They recommend Montecarlo methods
Combined
The aim of science is
not
to open the door to infinite wisdom,
but to set a limit to
infinite error
Bertolt Brecht, Life of Galileo (1939)