Class 27: Binomial Distribution
Methodology of Scientific Research
Andrés Aravena, PhD
May 9, 2023
Probability Distribution
Let’s say that \(Ω=\{a_1, a_2, …,a_n\}\)
We showed that the sum of all outcomes’ probabilities is 1 \[ℙ(\{a_1\}) + ℙ(\{a_2\}) + … + ℙ(\{a_n\})=1\] If we know these values, we can calculate everything.
The for all \(i\) \[p(a_i) = ℙ(\{a_i\})= ℙ(\text{outcome is exactly }a_i)\] is called the distribution of the probability.
It has two parts
This definition makes sense only if we agree on what are all the possible outcomes.
In other words, we must agree on what is \(Ω\)
Then the probability distribution is a function \[p: Ω → [0,1]\]
Notice that there may be more than one way to define \(Ω\)
Probabilities as proportions
Let’s assume that we know how many cards of each color are in the deck
There are \(n_c\) cards of color \(c\in\){“red”,“green”,“blue”, “yellow”}
There are \(N=∑ n_c\) cards in total
Indifference principle
If we do not have any solid reason to expect any particular order of cards, then each individual card has the same probability \(1/N\)
The probability of “first color \(c\)” is \[ℙ(\text{color is }c)=\frac{n_c}{N}\]
Probability of the next card
We will continue drawing cards, so the proportions will change
Let’s say we got color \(c_1\) in the first draw
Now we have \(N-1\) cards in total, and there are \(n_{c_1}-1\) cards of color \(c_1\)
The probability of “second color \(c\)” is
\[ℙ(\text{second color is }c|\text{first color is }c_1)=\begin{cases} \frac{n_c}{N-1} &\text{if }c≠c_1\\ \frac{n_c-1}{N-1} &\text{if }c=c_1 \end{cases}\]
It gets complicated
Making life easier
The formula applies when our measurement changes the experiment
There are two exceptions where proportions do not change
- If every \(n_c\) is large, then
\(n_c-1≈ n_c\) and \(N-1 ≈ N\)
- This is the case when we interview a few people from a large population
- If we put the card back into the deck and shuffle it again
- This is called sampling with replacement
In practice, we are often sample from a very large population and we model it as a sampling with replacement
Independent, Identically Distributed
If we replace the card into the deck after we see it, we will have
\[ℙ(\text{second color is }c|\text{first color is }c_1)=ℙ(\text{color is }c)=\frac{n_c}{N}\]
Notice that this means that the second result is independent of the first result, and so on
Moreover, the distribution is identical in each case
This is a very important case, and we give it a name
Independent, Identically Distributed (i.i.d.)
Simple case: a coin
- Has 2 sides: \(\Omega=\{\text{'Head'}, \text{'Tail'}\}\)
- Distribution given by \(ℙ(\text{'Head'})\) and \(ℙ(\text{'Tail'})\) such that \[ℙ(\text{'Head'}) + ℙ(\text{'Tail'})= 1\]
All can be reduced to the value \[p=ℙ(\text{'Head'})\]
We say that the probability distribution of the coin depends on the parameter \(p\)
Biased coin: cards
Real coins are usually fair, so \(p=0.5\)
We are interested in cases where \(p\) may be anything
This is the case when we have cards of two colors, with different proportions, and we do sampling with replacement
Still, we will call “coin” any experiment with two possible outcomes
(In math this is called a Bernoulli distribution)
Two coins
- There is only one way to get 0 heads: TT
- this happens with probability \(q^2\)
- There are two ways of getting 1 head: HT and TH
- this happens with probability \(pq\)
- There is only one way to get 2 heads: HH
- this happens with probability \(p^2\)
we get \[1⋅ q^2,\quad 2⋅ p q,\quad 1⋅ p^2\]
Three coins
- There is only 1 way to get 0 heads: TTT
- this happens with probability \(q^3\)
- There are 3 ways of getting 1 head: HTT, THT, and TTH
- this happens with probability \(pq^2\)
- There are 3 ways of getting 2 head: THH, HTH, and HHT
- this happens with probability \(p^2q\)
- There is only one way to get 3 heads: HHH
- this happens with probability \(p^3\)
we get \[1⋅ q^3,\quad 3⋅ pq^2,\quad 3⋅ p^2q,\quad 1⋅ p^3\]
This is like \((a+b)^2\)
The rule of combinations are the same as in the binomial theorem
We get \[ℙ(k\text{ Heads in }N\text{ coins})= \binom{N}{k} p^k q^{(N-k)}\]
The numbers \(\binom{N}{k}\) are found in Pascal’s triangle
Binomial formula
One way to remember it is to use the formula \[(p+q)^N =\sum_{k=0}^N \binom{N}{k} p^k q^{(N-k)}\]
This is why we call it Binomial distribution
Calculating \(ℙ(k\text{ Heads in }N\text{ coins})\)
We know that \[ℙ(K=k|N\text{ in total})=\binom{N}{k} p^k(1-p)^{n-k}\] We can calculate \(\binom{N}{k}\) using Pascal’s triangle, even in Excel
Binomial coefficient in Excel
Pascal’s Triangle 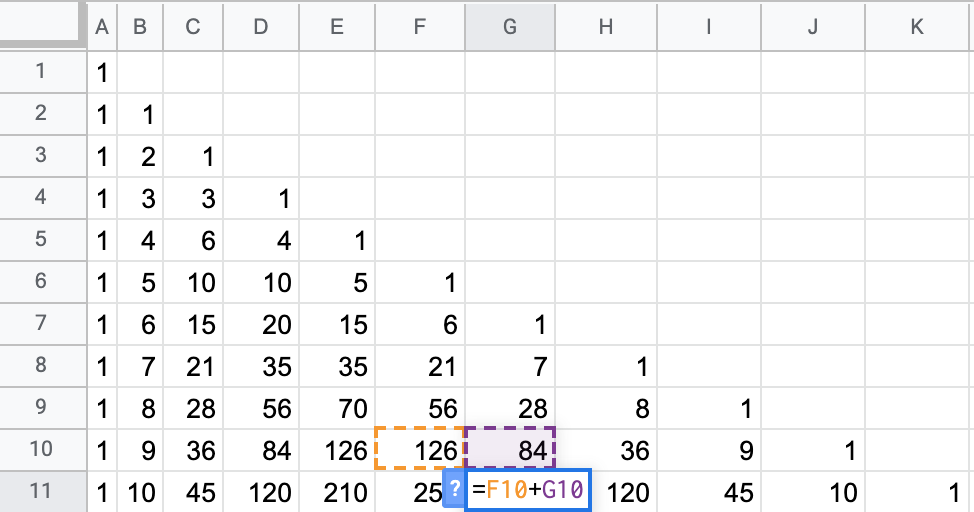
Binomial distribution in Excel
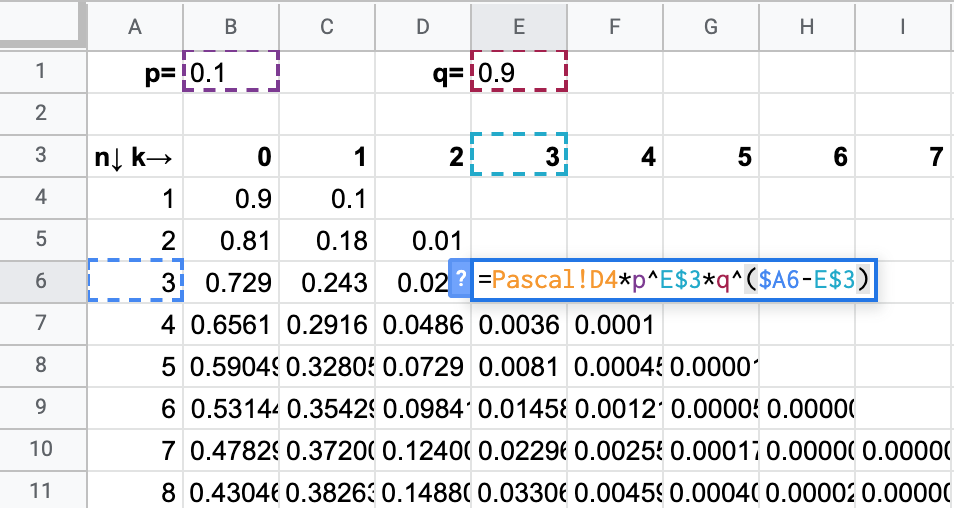
Binomial distribution visually
Cumulative distribution
\[ℙ(𝑆≤k)=\sum_{j=0}^k ℙ(𝑆=j)\]
Exercises
GC content of DNA fragment
We have a bacteria whose GC content is 38%
What is the GC content of a random DNA fragment of length 100bp?

How many persons with epilepsy in our course?
Worldwide proportion is 1%
And world is a population
We are 4 people in this course, including me
What is the probability that there are \(k\) persons with epilepsy in our class?
Three plants in a new environment
To test a new fertilizer, three plants were planted in a new environment
After one month, one died and the others survived
- What is the best estimation for the survival probability?
- What is the 95% interval for the survival probability?

