Class 23: Logical arguments
Methodology of Scientific Research
Andrés Aravena, PhD
April 28, 2023
Doing it backwards
In the last class we explored the truth value of \[A\text{ and }B \qquad A\text{ or }B\] when we know the truth value of \(A\) and of \(B\)
Now we want to go in the other direction
Is \(A\) true?
Assume that we know that \[A\text{ and }B\] is true
What can we say about \(A\)? And about \(B\)?
The negation of and
Assume that we know that \[\text{not }(A\text{ and }B)\] is true. In other words \[A\text{ and }B\] is false.
What can we say about \(A\)? and about \(B\)?
Is \(B\) true?
Assume that we know that \[A\text{ or }B\] is true
What can we say about \(A\)? And about \(B\)?
Combining two statements
We can see all possible ways to combine two statements with a double entry table like this one
| F | T | |
|---|---|---|
| F | . | . |
| T | . | . |
The first statement uses rows, the second uses columns
The logic operator depends on the four values of the table
Example: “and”
For the “and” operator, we have
| F | T | |
|---|---|---|
| F | F | F |
| T | F | T |
Do you agree?
The table does not change if we interchange rows and columns
What does that mean?
Exercise
Write the double entry table for “or”
Write the double entry table for “xor”
An interesting and important case
Consider this double entry table
| F | T | |
|---|---|---|
| F | T | T |
| T | F | T |
This table represents an operation called implication
What is the interpretation?
If is true that \(A\text{ implies }B\), what can we say about \(A\) and \(B\)
Conditional statement
We represent this statement with the symbol \(⇒\)
We write \(A⇒B\)
| F | T | |
|---|---|---|
| F | T | T |
| T | F | T |
If \(A\) (represented in the rows) is True then \(B\) must also be True
Otherwise the statement \(A⇒B\) would be false
Antecedent and Consequent
Notice that the matrix is not symmetric, thus the operation is not commutative
The order is important. Each part has a name
In the sentence \(A\text{ implies }B\)
- \(A\) is the antecedent or the hypothesis
- \(B\) is the consequent or the conclusion
Other names
- \(A\) implies \(B\)
- If \(A\), then \(B\)
- \(A\) is sufficient for \(B\)
- \(B\) is necessary for \(A\)
- \(A\) is a sufficient condition for \(B\)
- \(B\) is a necessary condition for \(A\)
Examples
- “If it is sunny, then we will go to the beach.”
- “If the sky is clear, then we will be able to see the stars.”
- “Studying for the test is a sufficient condition for passing the class.”
Even more names
- \(B\) if \(A\)
- \(B\) when \(A\)
- \(A\) only if \(B\)
- \(B\) whenever \(A\)
- \(B\) follows \(A\)
In set theory
If we have \[x∈P ⇒ x∈Q\] then, in set theory language, we can write \[P⊂Q\]
That is, \(P\) is a subset of \(Q\)
Biconditional Statement
If \(A⇒B\) and \(B⇒A\) we can write \(A⇔B\)
We say
- \(A\) if and only if \(B\)
- \(A\) is necessary and sufficient for \(B\)
- If \(A\) then \(B\), and conversely
- \(A\) iff \(B\), where “iff” stands for “if and only if”
This is true when \(A\) and \(B\) have the same truth values.
Logical equivalences and properties
Contraposition
\[A ⇒ B\] is equivalent to \[\text{not } B ⇒ \text{not } A\]
Or-and-if
\[A ⇒ B\] is equivalent to \[(\text{not } A )\text{ or }B\]
Negated conditionals
\[\text{not }(A ⇒ B)\] is equivalent to \[A \text{ and }\text{not } B\]
Import-Export
\[A ⇒ (B ⇒ C)\] is equivalent to \[(A \text{ and } B) ⇒ C\]
Commutativity of antecedents
\[\left(A ⇒ (B ⇒ C)\right)\] is equivalent to \[\left(B ⇒ (A ⇒ C)\right)\]
Distributivity
\[\left(C ⇒ (A ⇒ B)\right)\] is equivalent to \[\left((C ⇒ A) ⇒ (C ⇒ B)\right)\]
How math works
Axioms, Theorems and Proofs
In math we look for theorems. They all are like
If A is true and B is true then C is true
In other words, theorems are implications
To prove that a theorem is true, we need to see all the small implications
The axioms are statements that we assume to be true. They are the starting point of theorems
Example: Euclidean geometry
- Given two points, there is a straight line that joins them.
- A straight line segment can be prolonged indefinitely.
- A circle can be constructed when a point for its centre and a distance for its radius are given.
- All right angles are equal.
- If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, will meet on that side on which the angles are less than the two right angles.
Euclid believed these assumptions were intuitive
Example of theorem
From these axioms, Euclid proved that
- If two polygons have sides of the same length, then the two polygons have the same area
This is valid in particular for triangles and squares, because
- triangles and squares are polygons
A more famous theorem
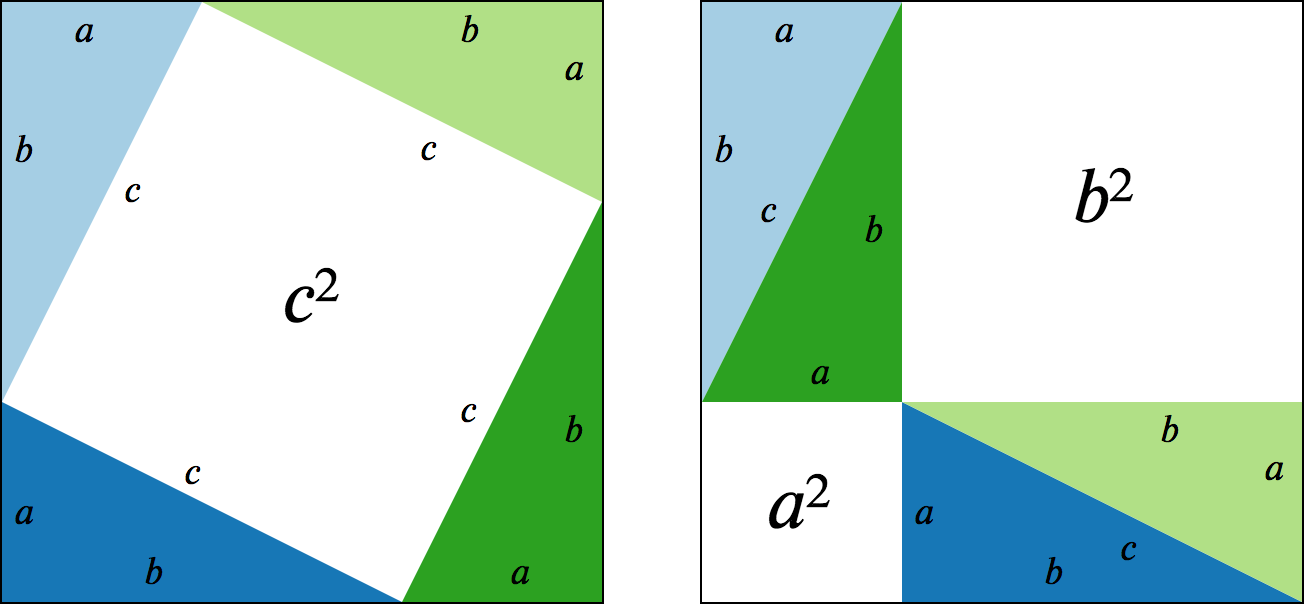
- Area of first square is \(2ab+c^2\)
- Area of the second square is \(a^2+2ab+b^2\)
- Both squares have the same area \((a+b)^2\)
People say that Pythagoras said
If is true that
- Area of first square is \(2ab+c^2\)
- Area of the second square is \(a^2+2ab+b^2\)
- Both squares have the same area \((a+b)^2\)
Then (8) and (9) and (10) imply that \[2ab+c^2 = a^2+2ab+b^2\] and therefore \[c^2 = a^2+b^2\]
Proof by contradiction
If \(A⇒B\) and we can show that \(B\) is false, we have proved that \(A\) is false. There is a famous example
Pythagoras theorem says that a right triangle with sides of length 1 has an hypotenuse of length \(\sqrt{2}\)
Greeks believed that all numbers were rational (i.e. like \(p/q\))
A student of Pythagoras used a proof by contradiction to show that \(\sqrt{2}\) cannot be rational (i.e. cannot be written as a fraction)
The legend says that his classmates killed him because of this
Schema of the proof by contradiction
Assume that \(\sqrt{2}=p/q\) with \(p\) and \(q\) natural numbers
Assume also that \(p\) and \(q\) don’t have common factors
Squaring both sides, we have \(2q^2=p^2\)
Therefore \(p^2\) is even. Thus \(p\) is even, and \(p=2r\)
Thus, \(2q^2=4 r^2\), which implies \(q^2=2r^2\)
Therefore \(q\) is even. And (4) says that \(p\) is also even
But this cannot be true, because of (2)
Therefore (1) must be false. \(\sqrt{2}\) cannot be a fraction
Validity of arguments
Valid arguments
An argument is a phrase saying that IF several predicates (called premises) are true, THEN another predicate (called conclusion) must also be true
All the premises are connected by AND
The argument is valid if it is a tautology
If the argument is not correct, we say it is a fallacy
Example
These examples are taken from The Internet Encyclopedia of Philosophy
- Elizabeth owns either a Honda or a Toyota
- Elizabeth does not own a Honda
- Therefore, Elizabeth owns a Toyota
\[((Honda \text{ or } Toyota) \text{ and } \text{not } Honda) ⇒ Toyota\]
Notice that the argument is valid even if Elizabeth as no car
Another example
- All toasters are made of gold.
- All things made of gold are time-travel machines
- Therefore, all toasters are time-travel machines
\[\begin{aligned}(Toaster ⇒ Gold) \text{ and } (Gold⇒ TimeMachine)\\ ⇒ (Toaster ⇒ TimeMachine)\end{aligned}\]
The first two propositions are not true
Nevertheless if they were true, the third proposition is necessarily true
Validity and Soundness
An argument may be valid even if the premises are never true
A argument is sound if and only if it is both valid, and all of its premises are actually true.
An invalid argument is a logical fallacy. Be aware of them!
See also:
Some important arguments
We saw that \((P\vee Q) \text{ and } \text{not } P) ⇒ Q\) and \[(P⇒ Q) \text{ and } (Q⇒ R)⇒ (P⇒ R)\] We also have “modus ponens” \[((P⇒ Q) \text{ and } P)⇒ Q\] and “modus tollens” \[((P⇒ Q) \text{ and } \text{not } Q)⇒ \text{not } P\]
Example of modus ponens
If being rich makes you happy and you are rich, then you are happy
IF you being rich IMPLIES you being happy AND you are rich THEN you are happy
IF \(Rich⇒ Happy\) AND \(Rich\), THEN \(Happy\)
\[((P⇒ Q) \text{ and } P)⇒ Q\]
Example of modus tollens
If being rich makes you happy and you are unhappy, then you are not rich
IF you being rich IMPLIES you being happy AND you are not happy THEN you are not rich
IF \(Rich⇒ Happy\) AND \(\text{not } Happy\), THEN \(\text{not } Rich\)
\[((P⇒ Q) \text{ and } \text{not } Q)⇒ \text{not } P\]
Summary
- Logical implication is the most important tool of logic
- It is asymmetrical. \(A⇒B\) is
different from \(B⇒A\)
- People often confuse them. Don’t fool yourself
- To show that \(A⇒B\) is true, we must show that there are no cases where \(B\) is true and \(A\) is false
- IF Ali is at Istanbul THEN Ali is on Turkey
- If Ali is in Turkey, he may be at Istanbul or not
- IF Ali is not in Turkey, THEN he is not at Istanbul