Class 17: Exponential Models
Methodology of Scientific Research
Andrés Aravena, PhD
April 6, 2023
How cells grow
Cells in a culture grow every day
We want to know the number of cells every day: \(\text{ncell(t)}\)
Here \(t\) is the time in days.
We start with an initial number of cells, that we call \(\text{initial}\)
Each day, the number of cells increases by a factor \(\text{rate}\)
\[\text{ncell(t)} = \text{initial} \cdot \text{rate}^{t}\]
How can we model it?
Graphically
We cannot see what happens when values are small
Logarithmic scale (“semi–log”)
We can see better using a logarithmic vertical scale
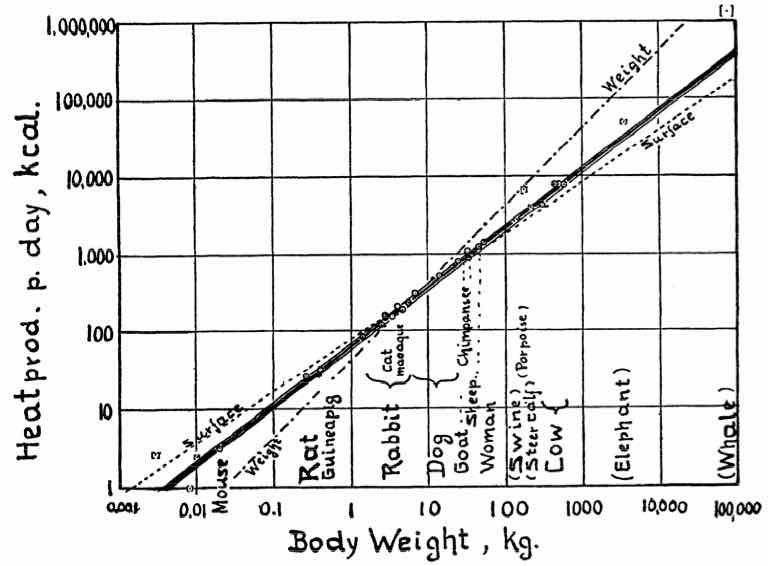
Relation of Body size v/s metabolic rate
Kleiber’s Law
(Physiological Reviews 1947 27:4, 511-541)
Same in semi–log scale
Third plot: log–log
Logarithms
What is a logarithm?
We need very little math: arithmetic, algebra, and logarithms
Just remember that if \(x=p^m\) then \[\log_p(x) = m\] For example \[\log_{10}(10000) = 4\]
We can change the base
If we use another base, for example \(q\), then \[\log_q(x) = \log_p(x) /\log_p(q)\] For example \[\begin{aligned} \log_2(10000) &= \log_{10}(10000)/\log_{10}(2)\\ \log_2(10000) &= 4/\log_{10}(2)\\ 13.28771 &= 4 / 0.30103 \end{aligned}\]
We can choose the best base
So if we use different bases, there is only a scale factor
The “easiest” one is natural logarithm
If \[x=\exp(m)\] then \[\log(x)=m\]
Other things about logarithms
They only work with positive numbers. Not with 0
If \(x=p\cdot q\) then \[\log(x)=\log(p)+\log(q)\]
If \(x=a^m\) then \[\log(x)=m\log(a)\]
Linear models can be used in three cases
Basic linear model \[y=A+B\cdot x\] Exponential change (Initial value and growth Rate) \[y=I\cdot R^x\] Power law (Constant and Exponent) \[y=C\cdot x^E\]
In other words
Basic linear model \[y=A+B\cdot x\] Exponential: if \(y=I\cdot R^x\) then \[\log(y)=\log(I)+\log(R)\cdot x\] Power of \(x\): if \(y=C\cdot x^E\) then \[\log(y)=\log(C)+E\cdot\log(x)\]
Which one to use?
The easiest way to decide is to
- draw several plots, placing log() in different places,
- see which one seems more like a straight line
For example, let’s analyze data from Kleiber’s Law
https://www.dry-lab.org/static/kleiber1947.txt
Exercise: Make all plots. Which plot seems more “straight”?
Which plot seems more “straight”?
The plot that seems more straight line is the log–log plot
Therefore we need a log–log model.
\[\log(\text{kcal})=β_0 + β_1 \cdot \log(\text{kg})\]
What is the interpretation of these coefficients?
If \(\log(\text{kcal})=4.21 + 0.756\cdot \log(\text{kg})\) then \[\text{kcal}=\exp(4.21) \cdot \text{kg}^{0.756} =67.1 \cdot \text{kg}^{0.756}\]
Therefore:
- For a 1kg animal, the average energy consumption is \(\exp(4.21) = 67.1\) kcal
- The energy consumption increases at a rate of \(0.756\) kcal/kg.
This is Kleiber’s Law
“An animal’s metabolic rate scales
to the ¾ power of the
animal’s mass”.
Google it
Prediction: What is wrong here?
| animal | kg | kcal | predicted |
|---|---|---|---|
| Mouse | 0.021 | 3.6 | 1.285 |
| Rat | 0.282 | 28.1 | 3.249 |
| Guinea pig | 0.410 | 35.1 | 3.532 |
| Rabbit | 2.980 | 167.0 | 5.031 |
| Cat | 3.000 | 152.0 | 5.036 |
| Macaque | 4.200 | 207.0 | 5.291 |
| Dog | 6.600 | 288.0 | 5.632 |
| animal | kg | kcal | predicted |
|---|---|---|---|
| Goat | 36.0 | 800 | 6.915 |
| Chimpanzee | 38.0 | 1090 | 6.955 |
| Sheep ♂ | 46.4 | 1254 | 7.106 |
| Sheep ♀ | 46.8 | 1330 | 7.113 |
| Woman | 57.2 | 1368 | 7.265 |
| Cow | 300.0 | 4221 | 8.517 |
| Young cow | 482.0 | 7754 | 8.876 |
Undoing the logarithm
We want to predict the metabolic rate, depending on the weight
The independent variable is \(\text{kg}\), the dependent variable is \(\text{kcal}\)
But our model uses only \(\log(\text{kg})\) and \(\log(\text{kcal})\)
So we have to undo the logarithm, using \(\exp()\)
Correct formula for prediction
| animal | kg | kcal | predicted |
|---|---|---|---|
| Mouse | 0.021 | 3.6 | 3.616 |
| Rat | 0.282 | 28.1 | 25.762 |
| Guinea pig | 0.410 | 35.1 | 34.185 |
| Rabbit | 2.980 | 167.0 | 153.113 |
| Cat | 3.000 | 152.0 | 153.889 |
| Macaque | 4.200 | 207.0 | 198.458 |
| Dog | 6.600 | 288.0 | 279.287 |
| animal | kg | kcal | predicted |
|---|---|---|---|
| Goat | 36.0 | 800 | 1007 |
| Chimpanzee | 38.0 | 1090 | 1049 |
| Sheep ♂ | 46.4 | 1254 | 1220 |
| Sheep ♀ | 46.8 | 1330 | 1228 |
| Woman | 57.2 | 1368 | 1429 |
| Cow | 300.0 | 4221 | 5001 |
| Young cow | 482.0 | 7754 | 7157 |
Visually (log–log scale)
Visually (linear scale)
In the paper
Exponential growth in Science and Technology
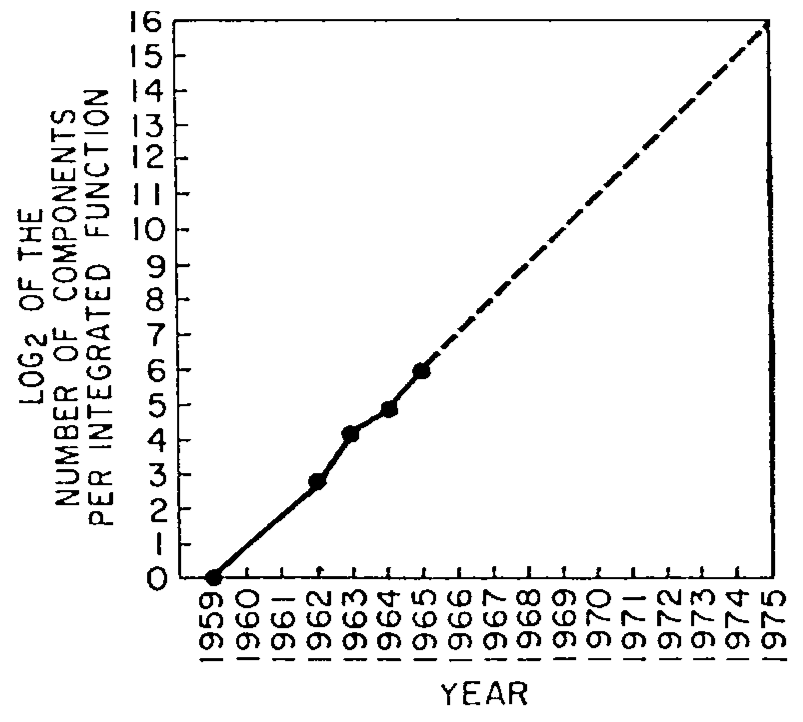
Moore’s Law

A idea from 1965, by George Moore (Intel)
The simple version of this law states that processor speeds will double every two years
More specifically, “the number of transistors on a CPU would double every two years”
(see paper)

Moore’s data and model
Intel says
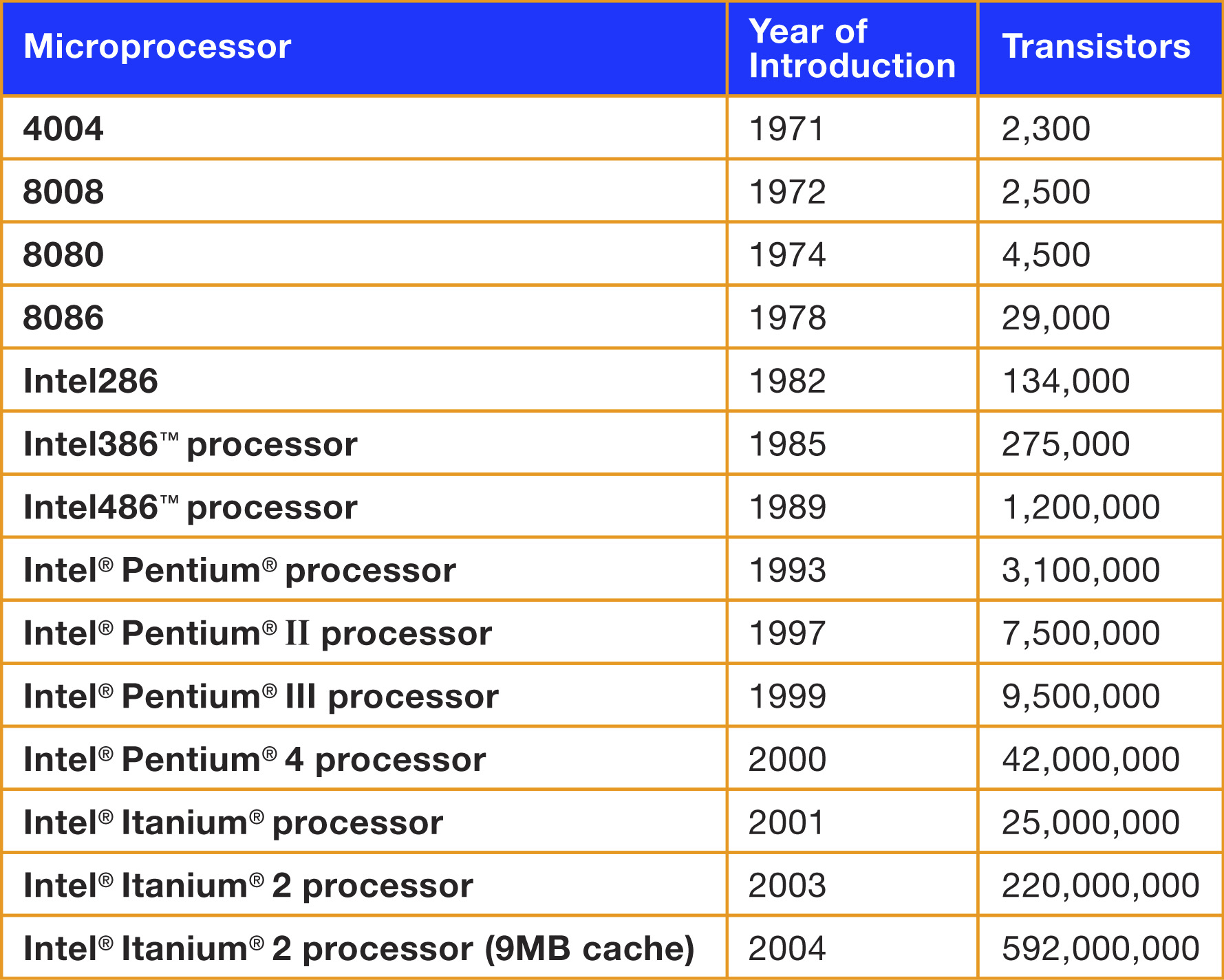
Real data: Number of transistors v/s year
Semi–log scale: Number of transistors v/s year
Computers get faster and faster
Definition of FLOPS
A ‘flops’ is a floating point operation per second
In simple words, is the number of multiplications per second that a computer can do
Same happens with DNA
Cost of sequencing human genome
Cost of sequencing human genome
Months since Sept 2000
Data for practice
https://www.dry-lab.org/static/Transistor_count.txt
What does this mean for you?
The Robots Are Coming
John Lanchester
An article in the “London Review of Books”
He tells this story
- 1992 Russo-American moratorium on nuclear testing
- Just after the Cold War
- 1996 Computer simulations to design new weapons
- Needed more computing power than could be delivered by any existing machine
The fastest computer of that time
USA designed ASCI Red, the first supercomputer doing over one teraflop
In 1997, ASCI Red did 1.8 teraflops
It was the most powerful supercomputer in the world until about the end of 2000.
In his article, John Lanchester says
“I was playing on Red only yesterday – I wasn’t really, but I did have a go on a machine that can process 1.8 teraflops.
“This Red equivalent is called the PlayStation3: it was launched by Sony in 2005 and went on sale in 2006.
Comparison of supercomputers
Red characteristics
- the size of a tennis court
- used as much electricity as 800 houses
- cost US$55 million.
The PS3
- fits under the TV,
- runs off a normal power socket,
- costs less than £200.
Things are changing fast
“[In 10 years], a computer able to process 1.8 teraflops went from being something that could only be made by the world’s richest government […], to something a teenager could expect [as a gift].
That was 15 years ago