Spies from another planet
(a science fiction story)
Arithmetic coding
Arithmetic coding is a way to represent a text using a
single real number
Each symbol is represented using a fixed number of digits.
- e.g. A↦01, B↦02, …,
space↦00 and so on
We put all numbers together and form a large number
Then we write 0. in front of the number and we get a
fraction
Arithmetic coding encodes the entire message into a single
number, a fraction q where 0.0 ≤ q < 1.0.
“Arithmetic coding” in WikiPedia
Example
Initial text
[1] "All Wikipedia"
Same, encoded as numbers:
[1] 33 76 76 0 55 73 75 73 80 69 68 73 65
Finally, in the form of a decimal fraction
[1] "0.3376760557375738069687365"
Physical encoding
![]()
An alien visited Earth, collected all observations in a big
file—let’s say, all Wikipedia
Then the alien encoded it using arithmetic code, resulting in a value
q
Finally, the alien took a 1 meter bar, and made a mark at q
meters
The bar is sent back to the alien country
What is the problem with this idea?
Uncertainty
Our tools have limited “resolution”
We cannot “resolve” the difference between small variations
![]()
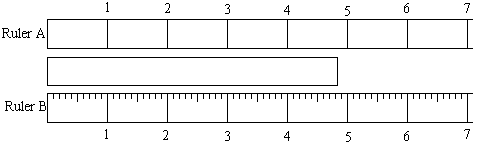
wpscms.pearsoncmg.com/wps/media/objects/1860/1905663/mathtutorial/rulers.gif
We need to know the resolution
We need to know the margin of error of our measurement
That is, how well we know the values
This is also called “precision”
Uncertainty must be declared
How big is the margin? How bad is the doubt?
We declare an interval: [xmin,
xmax]
Most of the time we write x ± 𝚫x
Example: 20cm ± 1cm
The aim of science
is
not to open the door to infinite wisdom,
but to set a limit to
infinite error
Bertolt Brecht, in “Life of Galileo” (1939)
Massive Stone Ball Discovered by Bosnian
In 2016 a large stone ball was found in Podubravlje village near
Zavidovici, Bosnia and Herzegovina.
![]()
Souvenirs for Tourists
![]()
We do not know how these stones were made
Similar stones have been found in Costa Rica
Nevertheless, people have made small round stones to sell as
souvenirs
Density of the stone ball
I was given a stone ball from Bosnia
We want to know its density
So we need to know mass and volume
- Estimate its mass
- Estimate its volume
- Estimate its density
Ask questions
Our estimation of mass
Based on intuition we think that the mass is more than 100gr and less
than 1Kg
Taking the geometric mean, we got 300gr
But it can be anything between 200gr and 400gr
We write 300gr ± 100gr
Our estimation of volume
Comparing with a tea cup, we guess 80ml
But it can be anything between 70ml and 90ml
We write 80ml ± 10ml
How would you estimate the density?
