Class 3: Distance
Bioinformatics
Andrés Aravena
September 29, 2022
Genetic code is a function
A function is a rule connecting each element of one set to one element of another set
Sometimes they are written with formulas
Sometimes they are written case-by-case
Example: NCBI
There’s a function connecting PubMed ids to PubMed records
Each PubMed ID points to one, and only one, PubMed record
The same is true for Nucleotide database, and protein database
(Obviously with different sets on each case)
Writing the genetic code
TTT F Phe TCT S Ser TAT Y Tyr TGT C Cys
TTC F Phe TCC S Ser TAC Y Tyr TGC C Cys
TTA L Leu TCA S Ser TAA * Ter TGA * Ter
TTG L Leu i TCG S Ser TAG * Ter TGG W Trp
CTT L Leu CCT P Pro CAT H His CGT R Arg
CTC L Leu CCC P Pro CAC H His CGC R Arg
CTA L Leu CCA P Pro CAA Q Gln CGA R Arg
CTG L Leu i CCG P Pro CAG Q Gln CGG R Arg
ATT I Ile ACT T Thr AAT N Asn AGT S Ser
ATC I Ile ACC T Thr AAC N Asn AGC S Ser
ATA I Ile ACA T Thr AAA K Lys AGA R Arg
ATG M Met i ACG T Thr AAG K Lys AGG R Arg
GTT V Val GCT A Ala GAT D Asp GGT G Gly
GTC V Val GCC A Ala GAC D Asp GGC G Gly
GTA V Val GCA A Ala GAA E Glu GGA G Gly
GTG V Val GCG A Ala GAG E Glu GGG G Gly A shorter representation
For our purposes each genetic code is a vector indexed by codons
AAs = FFLLSSSSYY**CC*WLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
Starts = ---M------**--*----M---------------M----------------------------
Base1 = TTTTTTTTTTTTTTTTCCCCCCCCCCCCCCCCAAAAAAAAAAAAAAAAGGGGGGGGGGGGGGGG
Base2 = TTTTCCCCAAAAGGGGTTTTCCCCAAAAGGGGTTTTCCCCAAAAGGGGTTTTCCCCAAAAGGGG
Base3 = TCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAGThe symbol ’*’ represents a stop codon
The line Starts = shows codons encoding start
(we will ignore the start codon information for now)
All genetic codes are similar
01 FFLLSSSSYY**CC*WLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
02 FFLLSSSSYY**CCWWLLLLPPPPHHQQRRRRIIMMTTTTNNKKSS**VVVVAAAADDEEGGGG
03 FFLLSSSSYY**CCWWTTTTPPPPHHQQRRRRIIMMTTTTNNKKSSRRVVVVAAAADDEEGGGG
04 FFLLSSSSYY**CCWWLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
05 FFLLSSSSYY**CCWWLLLLPPPPHHQQRRRRIIMMTTTTNNKKSSSSVVVVAAAADDEEGGGG
06 FFLLSSSSYYQQCC*WLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
09 FFLLSSSSYY**CCWWLLLLPPPPHHQQRRRRIIIMTTTTNNNKSSSSVVVVAAAADDEEGGGG
10 FFLLSSSSYY**CCCWLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
11 FFLLSSSSYY**CC*WLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
12 FFLLSSSSYY**CC*WLLLSPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
13 FFLLSSSSYY**CCWWLLLLPPPPHHQQRRRRIIMMTTTTNNKKSSGGVVVVAAAADDEEGGGG
14 FFLLSSSSYYY*CCWWLLLLPPPPHHQQRRRRIIIMTTTTNNNKSSSSVVVVAAAADDEEGGGG
16 FFLLSSSSYY*LCC*WLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
21 FFLLSSSSYY**CCWWLLLLPPPPHHQQRRRRIIMMTTTTNNNKSSSSVVVVAAAADDEEGGGG
22 FFLLSS*SYY*LCC*WLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
23 FF*LSSSSYY**CC*WLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
24 FFLLSSSSYY**CCWWLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSSKVVVVAAAADDEEGGGG
25 FFLLSSSSYY**CCGWLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
26 FFLLSSSSYY**CC*WLLLAPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
27 FFLLSSSSYYQQCCWWLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
28 FFLLSSSSYYQQCCWWLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
29 FFLLSSSSYYYYCC*WLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
30 FFLLSSSSYYEECC*WLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
31 FFLLSSSSYYEECCWWLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
33 FFLLSSSSYYY*CCWWLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSSKVVVVAAAADDEEGGGGWhat do we mean by similar?
When are two sequences similar?
Genetic codes are different
We compare them by counting how many times they are different
01 FFLLSSSSYY**CC*WLLLLPPPPHHQQRRRRIIIMTTTTNNKKSSRRVVVVAAAADDEEGGGG
02 FFLLSSSSYY**CCWWLLLLPPPPHHQQRRRRIIMMTTTTNNKKSS**VVVVAAAADDEEGGGGHow many symbols are different?
Calculating a distance between strings
First idea:
We count the number of mismatches
Both strings must have the same length
ASELLKYLTT ASELLKALTT
Here
distance(ASELLKYLTT,ASELLKALTT)
is 1
This is called Hamming distance
Hamming was a smart guy

- Manhattan Project
- programmed the IBM calculating machines
- Bell Telephone Laboratories
- involved in nearly all of the most prominent achievements
- Turing Award in 1968 (“Nobel Prize of Computer Science”)
Hamming distance examples
How many substitutions we need to go from one sequence to the other
CATandCAThave a Hamming distance of 0CATandBAThave a Hamming distance of 1CATandBAGhave a Hamming distance of 2
What if sequences have different length?
In that case we need to insert “gaps”
MOUSE
GROUSEPlacing two sequences face to face, inserting gaps if necessary is called Pairwise Alignment
There are many ways to insert gaps
The distance depends on the gaps positions
-MOUSE
GROUSEHamming Distance = 2
MOUSE--
-GROUSEHamming Distance = 7
So, which one is the distance?
In geometry we say that “the distance between a point X and a line L is the length of the shortest path from X to any point in L”
Same idea
If there many “candidate distances”, we choose the smallest one
This is an important idea
Distance is the length of the shortest path
Now we also count gaps
Hamming distance counts substitutions between sequences
Now we counts substitutions, insertions and deletions
This is called Levenstein distance
Hamming versus Levenstein
Hamming distance counts substitutions
ABCDEFGHIJ
BCDEFGHIJAHamming distance=10
Levenstein counts substitutions, insertions and deletions
ABCDEFGHIJK-
-BCDEFGHIJKALevenstein distance=2
What is the best way to insert gaps?
If the sequence has m letters, there are 2m+1 ways to insert a single gap
CAT
CAT-
CA-T
CA-T-
C-AT
C-AT-
C-A-T
C-A-T--CAT
-CAT-
-CA-T
-CA-T-
-C-AT
-C-AT-
-C-A-T
-C-A-T-And that is not even counting larger gaps
We could also do
C--A-----Tor
----CA-T--or
-C--A--T--There is a better way to find the best
We will see more details later
The idea is to draw a rectangle
- One sequence in the rows
- Another sequence in the columns
- Mark the cells where row letter and column letter are equal
It looks like this
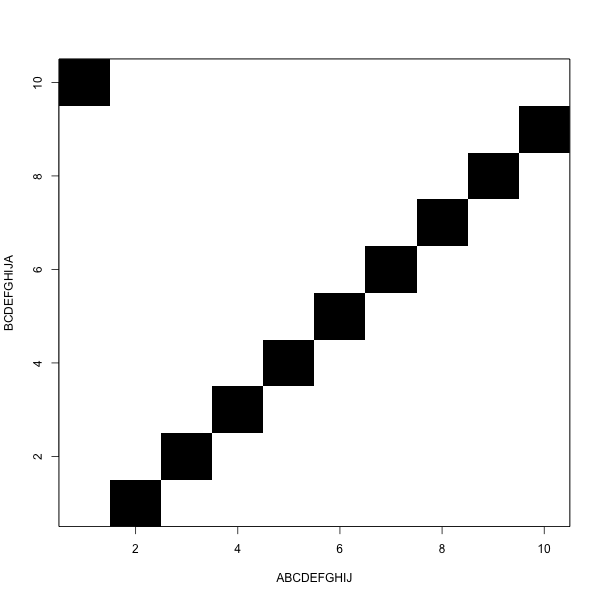
The goal is to move from one corner to the other
Jumping black to black is free
Horizontal and vertical moves are gaps
We move from one corner to the other
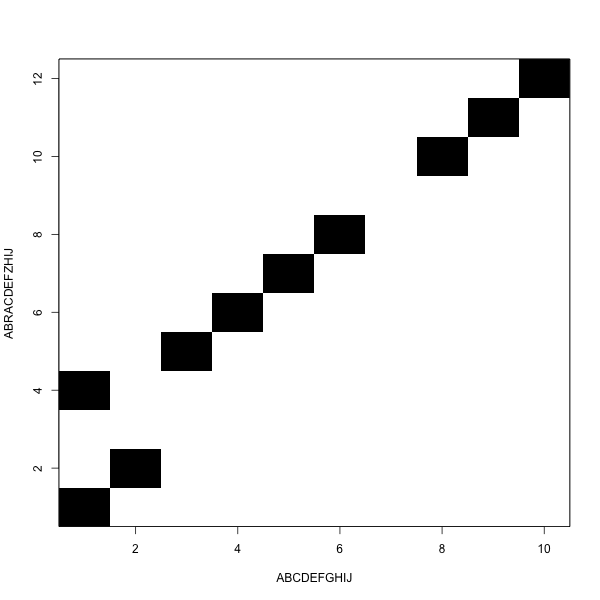
White blocks add to the distance
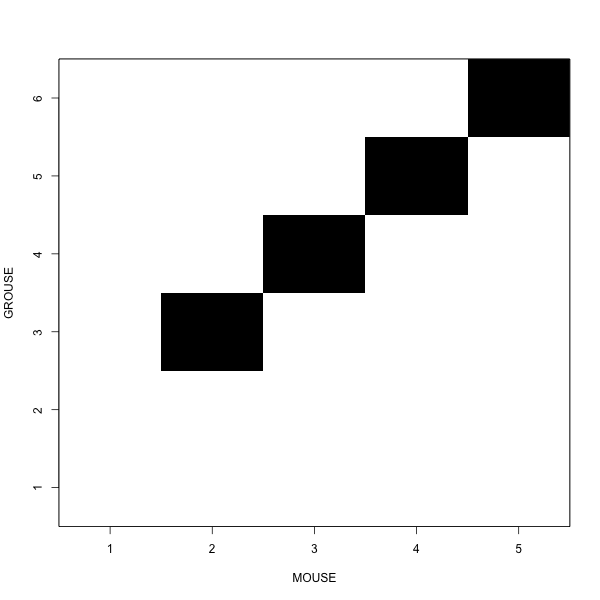
Summary
- Hamming distance
- Levenstein distance
- Dot plot