Class 21: Central Limit Theorem

Computing for Molecular Biology 2

Andrés Aravena, PhD

28 May 2021

Francis Galton, his cousin and his machine

Francis Galton

English explorer, Inventor, Anthropologist
(1822–1911)

Francis Galton

  • Cousin of Charles Darwin

  • He studied medicine and mathematics at Cambridge University.

  • He invented the phrase “nature versus nurture”

  • In his will, he donated funds for a professorship in genetics to University College London.

Galton Machine

Simulated Galton Machine

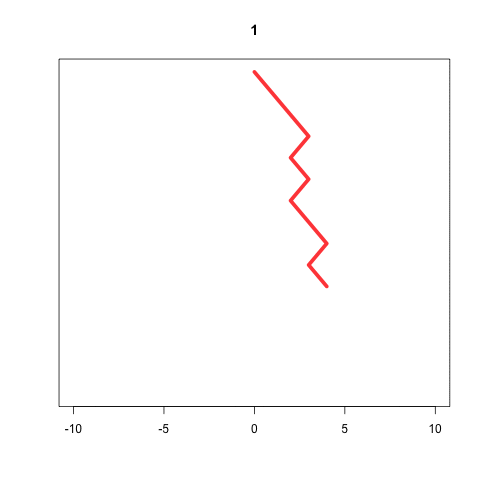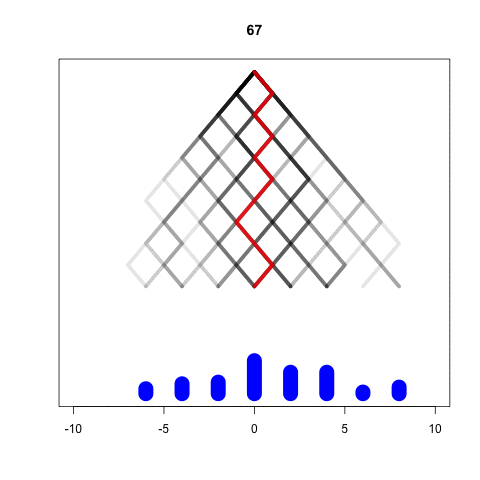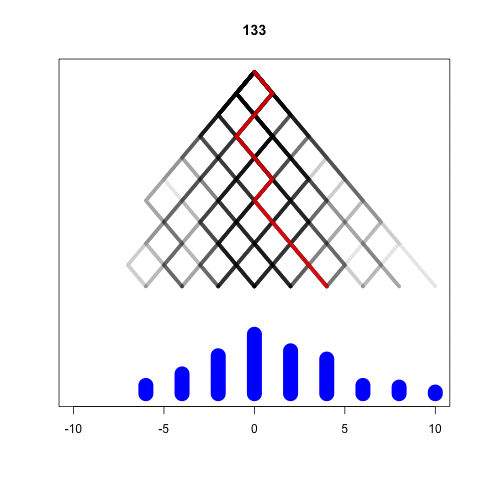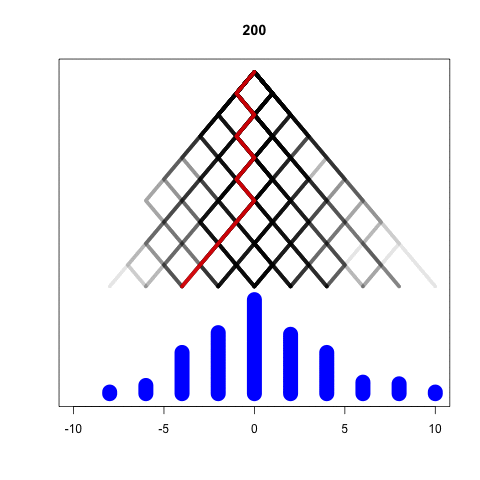
Simulating the Galton Machine

We take each ball independently

In every level, the ball bounces either left or right

We represent these options as -1 and 1

At the last level the position is the sum of all bounces

Simulating the Galton Machine

We will simulate each ball one by one

one_ball <- function(M) {
    bounces <- sample(c(-1, 1), size=M, replace=TRUE)
    return(sum(bounces))
}

Here M is the number of “left-right” choices made by the ball

In other words, M is the number of levels

Simulating the Galton Machine

Galton <- replicate(1000, one_ball(M=5))
barplot(table(Galton))

Larger M, larger variance

Galton <- replicate(10000, one_ball(M=50))
barplot(table(Galton))

Bigger M gives wider results

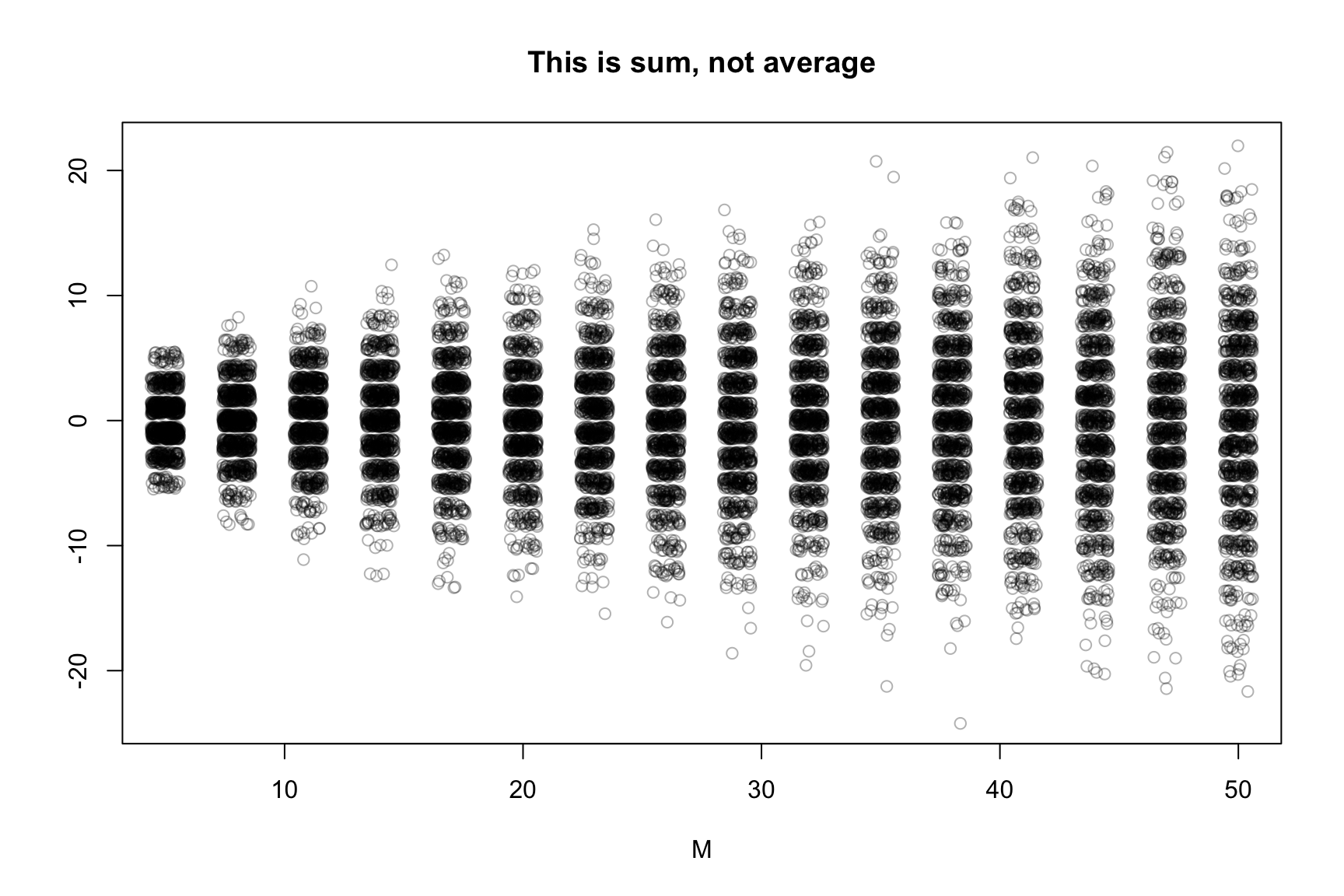
How Variance Grows

Better use log-log scale

Mean and Variance

It is easy to see that the population mean is 0 for any M

The previous plot shows that the variance is M

Thus, standard deviation will be sqrt(M)

correcting variance for M=5

Galton <- replicate(10000, one_ball(5))/sqrt(5)
barplot(table(Galton))

Notice that the x is not an integer anymore

correcting variance for M=50

Galton <- replicate(10000, one_ball(50))/sqrt(50)
barplot(table(Galton))

correcting variance for M=500

Galton <- replicate(100000, one_ball(500))/sqrt(500)
barplot(table(Galton))

correcting variance for M=5000

Galton <- replicate(100000, one_ball(5000))/sqrt(5000)
barplot(table(Galton))

When M is big, we get Normal distribution

The Normal distribution

This “bell-shaped” curve is found in many experiments, especially when they involve the sum of many small contributions

  • Measurement errors
  • Height of a population
  • Scores on University Admission exams

It is called Gaussian distribution, or also Normal distribution

The Central Limit Theorem

“The sum of several independent random variables converges to a Normal distribution”

The sum should have many terms, they should be independent, and they should have a well defined variance

(In Biology sometimes the variables are not independent, so be careful)

Normal distribution

Here outcomes are real numbers

Any real number is possible

Probability of any \(x\) is zero (!)

We look for probabilities of intervals

Probabilities of Normal Distribution

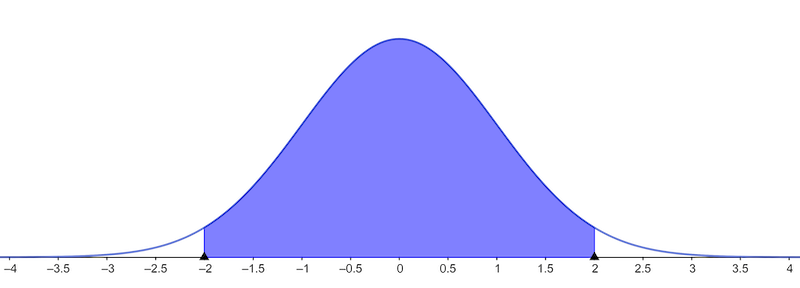
≈95% of normal population is between \(-2\cdot\text{sd}(\mathbf x)\) and \(2\cdot\text{sd}(\mathbf x)\)
≈99% of normal population is between \(-3\cdot\text{sd}(\mathbf x)\) and \(3\cdot\text{sd}(\mathbf x)\)

Simulating the Normal distribution

Instead of simulating the Galton machine several times, we can simulate the Normal distribution using the R function

rnorm(n, mean = 0, sd = 1)

The parameter n is mandatory. It is the sample size

You can also change the mean and the standard deviation of the simulation