Bertolt Brecht, Life of Galileo (1939)
March 4, 2020
The aim of science is not to open the door to infinite wisdom, but to set a limit to infinite error
What is a measurement?
- A measurement tells us about a property of something
- It gives a number to that property
- Measurements are always made using an instrument of some kind
- Rulers, stopwatches, weighing scales, thermometers, etc.
- The result of a measurement has two parts: a number and a unit of measurement
Measurement Good Practice Guide No. 11 (Issue 2). A Beginner’s Guide to Uncertainty of Measurement. Stephanie Bell. Centre for Basic, Thermal and Length Metrology National Physical Laboratory. UK
What is not a measurement?
There are some processes that might seem to be measurements, but are not. For example
- comparing two pieces of string to see which is longer
- Counting is not normally viewed as a measurement
- Tests that lead to a ‘yes/no’ answer or a ‘pass/fail’ result
However, measurements may be part of the process of a test
Measurements have uncertainty
Uncertainty of measurement is the doubt about the result of a measurement, due to
- resolution
- random errors
- systematic errors
Uncertainty must be declared
How big is the margin? How bad is the doubt?
- We declare an interval: [xmin, xmax]
- Most of the time we write x ± 𝚫x
- We declare the confidence level: how much we are sure that the real value is in this interval
Example: 20cm ± 1cm, at a level of confidence of 95%
Error versus uncertainty
Do not to confuse error and uncertainty
Error is the difference between the measured and the “true” value
Uncertainty is a quantification of the doubt about the result
Whenever possible we try to correct for any known errors
But any error whose value we do not know is a source of uncertainty
Where do errors and uncertainties come from?
Flaws in the measurement can come from:
- The measuring instrument – instruments can suffer from errors including bias, wear, drift, poor readability, noise, etc.
- The item being measured – which may not be stable (measure the size of an ice cube in a warm room)
- The measurement process – the measurement itself may be difficult to make. Measuring the weight of small animals presents particular difficulties
- ‘Imported’ uncertainties – calibration of your instrument has an uncertainty
Where do errors and uncertainties come from?
- Operator skill – One person may be better than another at reading fine detail by eye. The use of an a stopwatch depends on the reaction time of the operator
- Sampling issues – the measurements you make must be representative. If you are choosing samples from a production line, don’t always take the first ten made on a Monday morning
- The environment – temperature, air pressure, humidity and many other conditions can affect the measuring instrument or the item being measured
What is not a measurement uncertainty?
- Mistakes made by operators. They should not be counted as contributing to uncertainty. They should be avoided by working carefully and by checking work
- Tolerances. They are acceptance limits which are chosen for a process or a product.
- Specifications. A specification tells you what you can expect from a product.
Two ways to estimate uncertainties
- Type A - uncertainty estimates using statistics
- (usually from repeated readings)
- Type B - uncertainty estimates from any other information.
- past experience of the measurements, calibration certificates, manufacturer’s specifications, calculations, published information, common sense
In most measurement situations, uncertainty evaluations of both types are needed
Measurement Good Practice Guide No. 11 (Issue 2). A Beginner’s Guide to Uncertainty of Measurement.
Stephanie Bell. Centre for Basic, Thermal and Length Metrology National Physical Laboratory. UK
Reading v/s measurement
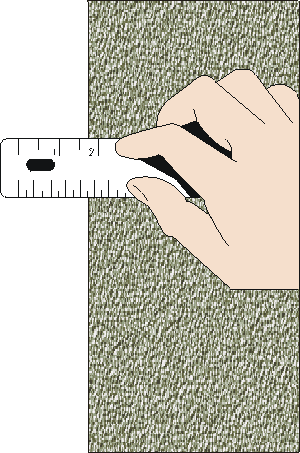
A reading is one observation of the instrument
A measurement may require several reads
For example, to measure a length, we make two reads, and we calculate the difference
The measurement will accumulate the uncertainty
Uncertainty of a single read
For a single read, the uncertainty depends at least on the instrument resolution
For example, my water heater shows temperature with 5°C resolution: 50, 55, 60,…
If it shows 55°C, the real temperature is somewhere between 53°C and 57°C
We write 55°C ± 2.5°C, with 100% confidence
For a single read, 𝚫x = half of the resolution
Combining Uncertainty
Sum of two measurements:
\[(x ± 𝚫x) + (y ± 𝚫y) = (x+y) ± (𝚫x+𝚫y)\]
Difference between measurements:
\[(x ± 𝚫x) - (y ± 𝚫y) = (x-y) ± (𝚫x+𝚫y)\]
Multiplying Uncertainty
To calculate \((x ± 𝚫x) \times (y ± 𝚫y)\) we first write the uncertainty as percentage
\[(x ± 𝚫x/x\%) \times (y ± 𝚫y/y\%)\]
Then we sum the percentages:
\[xy ± (𝚫x/x + 𝚫y/y)\%\]
Finally we convert back to the original units:
\[xy ± xy(𝚫x/x + 𝚫y/y)\]
Proof
\[ \begin{aligned} (x ± 𝚫x) \times (y ± 𝚫y) & = x(1 ± 𝚫x/x) \times y(1 ± 𝚫y/y)\\ & = xy(1 ± 𝚫x/x)(1 ± 𝚫y/y) \\ & = xy(1 ± 𝚫x/x ± 𝚫y/y ± (𝚫x/x)(𝚫y/y)) \\ & = xy(1 ± 𝚫x/x + 𝚫y/y) \\ & = xy ± xy(𝚫x/x + 𝚫y/y)\\ \end{aligned} \]
We discard \((𝚫x/x)(𝚫y/y)\) because it is small
We choose the pessimistic alternative on ±
Exercises
Measure the table top
First guess, then measure
- What is the length?
- What is the perimeter?
- What is the area?
- What is the volume?
Significant figures
Dinosaur Bones
Some tourists in the Museum of Natural History are marveling at some dinosaur bones. One of them asks the guard, “Can you tell me how old the dinosaur bones are?”
The guard replies, “They are 3 million, four years, and six months old.”
“That’s an awfully exact number,” says the tourist. “How do you know their age so precisely?”
The guard answers, “Well, the dinosaur bones were three million years old when I started working here, and that was four and a half years ago.”
Significant Figures
Lets be honest about what we know and what we do not know
We write the values that have real meaning
3 million years means 3±0.5 ⨉ 106
Adding 4.5 years is meaningless
It is the mark of an instructed mind to rest assured with that degree of precision that the nature of the subject admits, and not to seek exactness when only an approximation of the truth is possible
Aristotle (384–322 BC), Nicomachean Ethics