February 28, 2020
An operational definition of Science
What is “Measuring”
Measuring connect reality and math
Measuring takes an attribute from an object in nature and gives us a number
That is, measuring is a function from the real world into real numbers
Do not confuse measuring with calculating or evaluating
Can we measure 𝛑?
Observing, counting, measuring
These three ideas are similar, but different
- Observing leads to a nominal (or ordinal) scale
- Counting gives us a number from a nominal scale
- Measuring gives us an interval or ratio scale
What can be measured?
Things that can be measured
- Time
- Distances, areas, volumes
- speed, acceleration
- Mass, density
- Force, weight, work, energy, power
- Charge, current, voltage
- Heat, temperature, calories
- Information
- Money
- …
Units
Since all intervals are comparable, we measure an attribute by comparing it with a reference
Civilized countries use the Système international d’unités (SI)
- second (time)
- metre (length)
- kilogram (mass)
- ampere (electric current)
- kelvin (temperature)
- mole (amount of substance)
- candela (luminous intensity)
Instruments
Normally, measurements are based in the physical property we care
- Clock, timer
- Measuring rod (like the picture, Istanbul Archeological Museum)
- Balance and weights
Transducers and sensors
In some cases, it may be easy to measure an electrical signal depending on the attribute to be measured
"A transducer is a device that converts energy from one form to another.
Usually a transducer converts a signal in one form of energy to a signal in another"
Wikipedia
Examples
- pH probes
- Electro-galvanic oxygen sensors
- Accelerometers
- Load cells – converts force electrical signal
- Potentiometers (when used for measuring position)
- Pressure sensors
- Gyroscopes
Electroacoustic
- Microphones – converts sound into an electrical signal
- Piezoelectric crystals – converts deformations (vibrations) to and from electrical signals
- Geophones – ground movement into voltage
- Hydrophones – changes in water pressure into an electrical signal
- Ultrasonic transceivers – transmitting and receiving ultrasound, for imaging.
Photoelectric, Thermoelectric
Photodiodes, phototransistors, photomultipliers – converts changing light levels into electrical signals
Photodetector or photoresistor or light dependent resistor (LDR) – converts changes in light levels into changes in electrical resistance
Thermistors – converts temperature into electrical resistance
Thermocouples – converts relative temperatures of metallic junctions to electrical voltage
Radiation
Geiger-Müller tubes – converts incident ionizing radiation to an electrical impulse signal
Radio receivers converts electromagnetic transmissions to electrical signals.
Any cellphone
My first smartphone was a Nokia N95. It had
- Accelerometer (to rotate the screen)
- GPS
- Microphone
- Battery
- 3G, Wifi
- Programmable in Python
So I tried to build a seismological station
Today is much easier: https://phyphox.org/
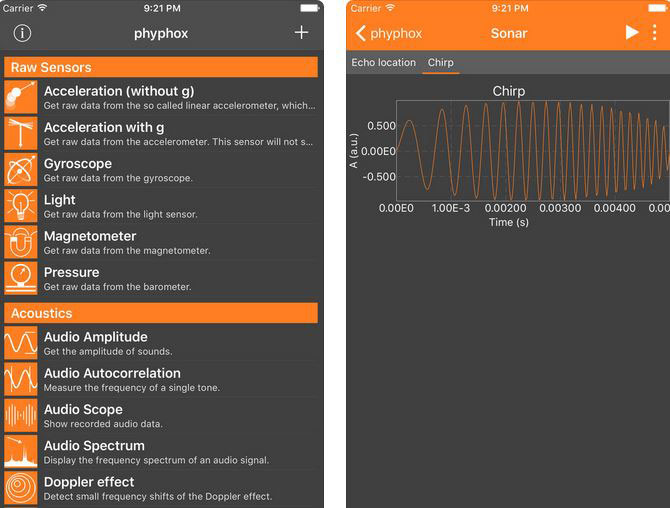
The Barometer Story
The first story I read in the University

In my first day of classes, the student union gave us a newspaper with this story in the first page:
The following concerns a question in a physics degree exam at the University of Copenhagen:
“How could you measure the height of a tall building, using a barometer?”
One students gave the following answers
“You tie a long piece of string to the neck of the barometer, then lower the barometer from the roof to the ground. The length of the string plus the length of the barometer will equal the height of the building.”
“Take the barometer up to the roof, drop it over the edge, and measure the time it takes to reach the ground. The height of the building can then be worked out from the formula h = gt2/2”
One students gave the following answers (2)
“If the sun is shining you could measure the height of the barometer, then set it on end and measure the length of its shadow. Then you measure the length of the building’s shadow, and thereafter it is a simple matter of proportional arithmetic to work out the height”
“But if you wanted to be highly scientific about it, you could tie a short piece of string to the barometer and swing it like a pendulum, first at ground level and then on the roof of the skyscraper. The height is worked out by the difference in the gravitational restoring force T =2 𝜋 √(l /g).”
One students gave the following answers (3)
Tying a piece of string to the barometer, which is as long as the height of the building, and swinging it like a pendulum, and from the swing period, calculate the pendulum length.
“Or if the skyscraper has an outside emergency staircase, it would be easier to walk up it and mark off the height of the skyscraper in barometer lengths, then add them up.”
One students gave the following answers (4)
“I would go to the building superintendent and offer him a brand-new barometer if he will tell me the height of the building!”
The expected answer: Measuring the pressure difference between ground and roof and calculating the height difference.
The story’s moral
The story shows that the same attribute can be measured through different physical properties
Thinking “out of the box” enables measuring things that were not easy to measure before
Spies from another planet
From Wikipedia
Arithmetic coding is […] used in lossless data compression.
Normally, a string of characters […] is represented using a fixed number of bits per character, as in the ASCII code. […]
Arithmetic coding […] encodes the entire message into a single number, an arbitrary-precision fraction q where 0.0 ≤ q < 1.0.
Example
Initial text
[1] "All Wikipedia"
Same, encoded as numbers:
[1] 33 76 76 0 55 73 75 73 80 69 68 73 65
Finally, in the form of a decimal number
[1] "0.3376760557375738069687365"
Physical encoding
An alien visited Earth, collected all observations in a big file—let’s say, all Wikipedia
Then the alien encoded it using arithmetic code, resulting in a value q
Finally, the alien took a 1 meter bar, and made a mark at q meters
The bar is sent back to the alien country
What is the problem with this idea?
Uncertainty
Our tools have limited “resolution”
We cannot “resolve” the difference between small variations
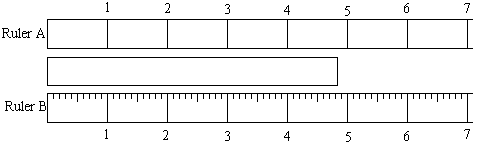
wpscms.pearsoncmg.com/wps/media/objects/1860/1905663/mathtutorial/rulers.gif
This can be solved with higher precision tools

Calipers
Observational error
With higher precision we get a new problem:
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case
- Random error which may vary from observation to another
Precision, accuracy, and trueness
In this context, people has defined the following ideas
- accuracy: closeness of measurements to the true value
- precision: closeness of the measurements to each other
- trueness: closeness of the mean of a set of measurement to the true value
BS ISO 5725-1: “Accuracy (trueness and precision) of measurement methods and results - Part 1: General principles and definitions.”, p.1 (1994)
Precision v/s trueness

High trueness, Low precision

High precision, Low tureness
In a graphic
.svg)
Historical note
In some old material, people say “accuracy” in place of trueness
Other people say bias
These words are still common in science and technology
Be aware of this discrepancy
The German way
Measure twice, cut once

The Chilean way
Measure once, cut twice

Knowing the uncertainty

Estimating uncertainty for a single measurement
The uncertainty of a single measurement is limited by the precision and accuracy of the measuring instrument, along with any other factors that might affect the ability of the experimenter to make the measurement.
Estimating the uncertainty
- Instrument resolution (random)
- Physical variations (random)
- Parallax (systematic or random)
Example
to measure the diameter of a tennis ball
- using a meter stick to measure the diameter of a tennis ball, the uncertainty might be ± 5 mm,
- using a Vernier caliper, the uncertainty could be ± 2 mm.
The limiting factor with the meter stick is parallax, while the second case is limited by ambiguity in the definition of the tennis ball’s diameter (it’s fuzzy!)
Example
In both of these cases, the uncertainty is greater than the smallest divisions marked on the measuring tool (likely 1 mm and 0.05 mm respectively)
Unfortunately, there is no general rule for determining the uncertainty in all measurements.
The experimenter is the one who can best evaluate and quantify the uncertainty of a measurement based on all the possible factors that affect the result.
Therefore, the person making the measurement has the obligation to make the best judgment possible and report the uncertainty in a way that clearly explains what the uncertainty represents
Exercise
Measure the length and width of the table
Next class
- Measure the speed of sound
- Measure the height of a building
- Error propagation
- Calibration
- Replicability
- Estimation
Homework
Read the short story “Funes the Memorious” (by Argentine writer Jorge Luis Borges). You can find it on the web.
- There is a PDF in Turkish language. Google “Funes ve Sonsuz Bellek” and look on pages 111-119.
- Write (paper, mail, whatever) the key ideas of the story
- In particular answer: Do you want to have perfect memory? Why?
