Long-term behavior and effect of initial conditions

May 5, 2020

Our course so far

Solve simple problems
- Decomposition
- Pattern matching
- Abstraction
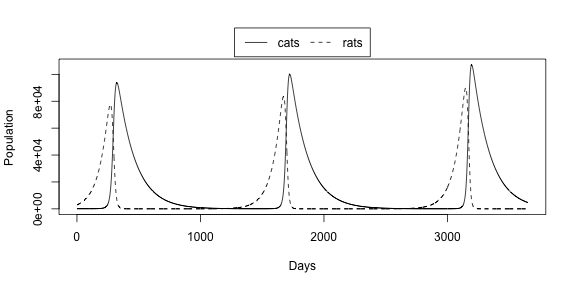
Systems Analysis
- Identify the system parts and processes
- Use R to simulate a system
- See what happens in the long term

Long term

One important question that we want to answer is

What happens in the long term

In may cases it is not easy to guess. Our intuition is bad

We need to simulate and see what happens

Polymerase Chain Reaction

The Polymerase Chain Reaction (PCR) is a method used to synthesize millions of copies of a given DNA sequence.

A typical PCR reaction consists of series of cycles:

template DNA denaturation,
primer annealing, and
extension of the annealed primers by DNA polymerase.

This loop is repeated between 25 and 30 times

PCR system

We simplify and we forget about the polymerase and the dNTP. They both will be represented by primers.

We have a system with two parts, DNA and primers and one process, the thermal cycle.

The system is represented by this diagram:

We have seen this before

This system was in Homework 8

Many of you noticed that this system has the same shape of cell-food system

Same shape means same behavior

Simulate several PCR cycles

Let’s write a function to simulate the PCR reaction.

The function name should be pcr and it must take four inputs:

the number of cycles N,
the initial DNA concentration DNA_ini,
the initial primer concentration primer_ini, and
the reaction rate cycle_rate.

The function must return a data frame with cycle, DNA and primer.

Simulate several PCR cycles

pcr <- function(N, DNA_ini, primer_ini, cycle_rate) {
    DNA    <- d_DNA    <- rep(NA, N)
    primer <- d_primer <- rep(NA, N)
    DNA[1] <- DNA_ini
    primer[1] <- primer_ini
    for(i in 2:N) {
        cycle <-  cycle_rate * primer[i-1] * DNA[i-1]
        d_DNA[i]    <-  cycle
        d_primer[i] <- -cycle
        DNA[i]    <-    DNA[i-1] + d_DNA[i]
        primer[i] <- primer[i-1] + d_primer[i]
    }
    return(data.frame(cycle=1:N, DNA, primer))
}

Simulate several PCR cycles

pcr(N=6, DNA_ini=1e6, primer_ini=1e8, cycle_rate=1e-8)

  cycle      DNA    primer
1     1  1000000 100000000
2     2  2000000  99000000
3     3  3980000  97020000
4     4  7841396  93158604
5     5 15146331  85853669
6     6 28150012  72849988

Simulate several PCR cycles

experiment <- pcr(N=20, DNA_ini=1e6, primer_ini=1e8,
                               cycle_rate=1e-8)
plot(DNA ~ cycle, experiment, type="o")

Long term behavior

The system reaches an equilibrium
Once the primers are finished, the reaction stops
We can see the final DNA and primer concentrations
Question: Does final DNA depends on
- initial DNA concentration?
- initial primer concentration?
- PCR reaction rate?

Effect of initial values

PCR depends on initial concentration

The PCR reaction curve depends on the initial concentration of DNA.

We want to understand this dependency for the following values of initial DNA concentration:

initial_DNA <- 10**(0:6)
initial_DNA

[1] 1e+00 1e+01 1e+02 1e+03 1e+04 1e+05 1e+06

PCR depends on initial concentration

for(i in 1:6) {
    experiment <- pcr(N=30, DNA_ini=initial_DNA[i],
                      primer_ini=1e8, cycle_rate=1e-8)
    plot(DNA ~ cycle, experiment, main=initial_DNA[i])
}

Result in next slide

PCR depends on initial concentration

All in one plot

Remember that each plot() command creates a new plot

We want to have only one plot

We will plot() the first result, the we will add lines() for the rest

PCR depends on initial concentration

experiment <- pcr(N=30, DNA_ini=initial_DNA[1],
                  primer_ini=1e8, cycle_rate=1e-8)
plot(DNA ~ cycle, data=experiment, type="o",
            main="Effect of initial DNA on PCR")
for(i in 2:length(initial_DNA)) {
    experiment <- pcr(N=30, DNA_ini=initial_DNA[i],
                      primer_ini=1e8, cycle_rate=1e-8)
    lines(DNA ~ cycle, experiment, pch=i, type="b")
}
legend("topleft", legend=initial_DNA, pch=1:7)

PCR depends on initial concentration

Quantitative PCR

Long term behavior is the same in all cases
- DNA concentration is saturated
- All primers are used
Initial DNA concentration changes when the saturation happens
- More initial DNA means faster reaction

Initial DNA concentration affects reaction time

We need to measure when DNA concentration increases a lot
One easy way to do that is to find in which cycle does the DNA concentration crosses the 50% line
We can use the function position_of_half() from Homework 6.

`position_of_half()` function

one solution for Homework 6

position_of_half <- function(x) {
    half_value <- (max(x)+min(x))/2
    for(i in 1:length(x)) {
        if(x[i]>= half_value) {
            return(i)
        }
    }
}

Example

DNA concentration crosses 50% at 21 cycles

Cycle Threshold

CT <- rep(NA, length(initial_DNA))
for(i in 1:length(initial_DNA)) {
    experiment <- pcr(N=30, DNA_ini=initial_DNA[i],
                    primer_ini=1e8, cycle_rate=1e-8)
    CT[i] <- position_of_half(experiment$DNA)
}

Result

We conclude that the CT value can be used to predict the initial DNA concentration.

Water formation

Water

A chemical reaction combines hydrogen and oxygen to produce water

To make it simple we will assume that the reaction is this:

2 H + O ↔ H₂O

Our system has 3 items:

Hydrogen
Oxygen
Water

Reactions are bidirectional

The items of the system

We represent hydrogen by H, oxygen by O, and water by W.

Each vector has the number of atoms or molecules for different times

We will measure the number of atoms and molecules in moles

The initial quantities are:

1 mole oxygen,
1 mole hydrogen, and
0 mole water

The rules are the following:

There are two reactions at the same time:

from hydrogen and oxygen into water
(that is, left to right),
from water into hydrogen and oxygen
(that is, right to left).

We also see that

The number water molecules increase with the first reaction and decreases with the second reaction
The number of oxygen atoms reduces with the first reaction and increases with the second
The number of hydrogen atoms reduces two times with the first reaction and increases two times with the second

Simplifying notation

According to our rules, we have two rates:

r1_rate
r2_rate

In chemistry, these rates are usually written as k₁ and k₂

We can see that

The speed of reaction r1 depends on the reaction rate, the number of oxygen atoms, and the square of the number of hydrogen atoms

r1_rate *  H * H * O

The speed of r2 depends on the reaction rate and the number of water molecules

r1_rate *  W

actual reaction rates depend on temperature and other conditions

Main part of simulation

for(i in 2:N) {
    r1 <- r1_rate*H[i-1]*H[i-1]*O[i-1]
    r2 <- r2_rate*W[i-1]
    d_W[i] <-   r1 - r2
    d_O[i] <-  -r1 + r2
    d_H[i] <- -2*r1 + 2*r2
    W[i] <- W[i-1] + d_W[i]
    O[i] <- O[i-1] + d_O[i]
    H[i] <- H[i-1] + d_H[i]
}

Exercise: finish it

Create a water_formation function.

Inputs are:

N: Number of steps in the simulation
H_ini: initial amount of hydrogen
O_ini: initial amount of oxygen
W_ini: initial amount of water
r1_rate: reaction 1 rate
r2_rate: reaction 2 rate

Exercise 2: conservation of mass

One atom of oxygen has 16 times the mass of one atom of hydrogen

Therefore one molecule of water has mass 18

Show that the total mass never changes

Long term behavior: equilibrium

mix <- water_formation(N=200, r1_rate=0.01, r2_rate=0.01,
     H_ini=2, O_ini=1, W_ini=0)

Equilibrium values depends on `r1_rate`

rates_of_r1 <- 10^seq(from=-3, to=-1, length=5)
r2_rate=0.01, H_ini=2, O_ini=1, W_ini=0

We can predict final outcome for each rate

rates_of_r1 <- 10^seq(from=-3, to=-1, length=5)
r2_rate=0.01, H_ini=2, O_ini=1, W_ini=0

Same with more `r1_rate` values

rates_of_r1 <- seq(from=0.001, to=0.1, length=50)
r2_rate=0.01, H_ini=2, O_ini=1, W_ini=0

This is the same pattern as CT on qPCR

final_Water <- rep(NA, length(rates_of_r1))
for(i in 1:length(rates_of_r1)) {
    mix <- water_formation(N=100, r1_rate=rates_of_r1[i],
                r2_rate=0.01, H_ini=2, O_ini=1, W_ini=0)
    final_Water[i] <- mix$Water[100]
}
plot(rates_of_r1, final_Water)

What was the reaction rate?

We can measure how much water we got. If at the end we have 0.5 mol of water, then …

… with the curve we can find what was the reaction rate

Other Long-Time Behavior

The two cases we saw had the same long-term behavior: equilibrium

Other systems (such as predator-prey model) can have other behavior: cycle

Key Questions

What is the long time behavior
- Equilibrium
- Cycle
- Chaos
What is the long-term effect of
- initial values
- process rates
If we know the long-term behavior, what was
- the initial values
- the process rates

Extra material

In the blog

Simulating Systems on the computer
Exercise: Predator-Prey System
- Focus only in the first question, about Lotka and Volterra

Our course so far

Long term

Polymerase Chain Reaction

Polymerase Chain Reaction

PCR system

We have seen this before

Simulate several PCR cycles

Simulate several PCR cycles

Simulate several PCR cycles

Simulate several PCR cycles

Long term behavior

Effect of initial values

PCR depends on initial concentration

PCR depends on initial concentration

PCR depends on initial concentration

All in one plot

PCR depends on initial concentration

PCR depends on initial concentration

Quantitative PCR

Initial DNA concentration affects reaction time

position_of_half() function

Example

Cycle Threshold

Result

Water formation

Water

Reactions are bidirectional

The items of the system

The rules are the following:

We also see that

Simplifying notation

We can see that

Main part of simulation

Exercise: finish it

Exercise 2: conservation of mass

Long term behavior: equilibrium

Equilibrium values depends on r1_rate

We can predict final outcome for each rate

Same with more r1_rate values

This is the same pattern as CT on qPCR

What was the reaction rate?

Other Long-Time Behavior

Key Questions

Extra material

`position_of_half()` function

Equilibrium values depends on `r1_rate`

Same with more `r1_rate` values