- Computational Thinking
- Decomposition
- Pattern Recognition
- Abstraction
- Algorithm Design
- Not about memory
- About Problem solving
April 7, 2020
What do you need to know?
Key ideas
- Loops:
for(){},while(){} - Conditional:
if(){},if(){} else {}
Practical tools
- Turtle graphics
- Normal graphics:
plot(),segments() - Reading DNA sequences
read.fasta()
Lessons from Homework
- Do it manually first
- Write in R and test
- Be careful with the syntax
if(){}has two parts: condition and command- Do not confuse index and content
- Try again and again
Homework is essential
- It is the only way to practice
- It is the only way to learn
- It gives me feedback on your learning
- It will make you a better professional
- It prepares you for the exam
Exams
- This years exams will be different from other years
- We need to be sure that each student gets the same chances
- We need to be sure that each answer is personal to the student
- We will be very strict with ethics
Analyzing DNA
DNA has two strands
FASTA files show only one strand
We call it the forward strand
The other strand is not shown, but can be calculated
We call it the reverse strand
Calculating the reverse strand
According to Watson & Crick, the reverse strand is complementary
- Change
abytand vice-versa - Change
cbygand vice-versa
Moreover, the reverse strand is reversed
- 5’ becomes 3’ and vice-versa
- i.e. we have to read it backwards
reverse_complement <- function(dna) {
for(i in 1:length(dna)) {
j <- length(dna) - i + 1
if(dna[i]=='a') {
answer[j] <- 't'
} else if(dna[i]=='c') {
answer[j] <- 'g'
} else if(dna[i]=='g') {
answer[j] <- 'c'
} else if(dna[i]=='t') {
answer[j] <- 'a'
}
}
return(answer)
}
Warning
There is something wrong here.
Create a vector before using it
We cannot use answer[i] if the vector answer does not exist
It has to be created before
We can create answer as a vector of NA values
answer <- rep(NA, size)
We have the new vector, but we don’t know yet the values
We need to know the vector’s size
We can create answer with this command
answer <- rep(NA, size)
For this, we need to know the size of the new vector
In this case it must be the same size as the dna vector
(because opposite strands have the same length)
reverse_complement <- function(dna) {
answer <- rep(NA, length(dna))
for(i in 1:length(dna)) {
j <- length(dna) - i + 1
if(dna[j]=='a') {
answer[i] <- 't'
} else if(dna[j]=='c') {
answer[i] <- 'g'
} else if(dna[j]=='g') {
answer[i] <- 'c'
} else if(dna[j]=='t') {
answer[i] <- 'a'
}
}
return(answer)
}
This is the correct version
Result
dna <-c('t','a','a','c','g','t')
dna
[1] "t" "a" "a" "c" "g" "t"
reverse_complement(dna)
[1] "a" "c" "g" "t" "t" "a"
DNA statistics
What happens if we use the reverse strand
Will GC–content change?
Will GC–skew change?
Answer
- GC–content does not change
- Because G+C does not change
- GC–skew changes sign
- Because G-C changes sign
- Because each C becomes a G and vice-versa
Local statistics
Statistics in parts of the genome
Local statistics look only through a small window
A Window is a part of the genome, from an initial position, and with a fixed size
For example, we can analyze a region of 500 bp starting at position 3000 of the genome
Looking at the window
The function seq() makes numeric sequences
window <- dna[seq(from=3000, length.out=500)]
In the general case, we can write
window <- dna[seq(from=start, length.out=size)]
Remember the seq() function
seq(from, to, by, length.out)
All inputs are optional
Choose carefully which ones to use
Examples of seq()
seq(from=5, to=14)
[1] 5 6 7 8 9 10 11 12 13 14
seq(from=5, length.out=10)
[1] 5 6 7 8 9 10 11 12 13 14
seq(from=5, to=30, by=3)
[1] 5 8 11 14 17 20 23 26 29
Evaluate gc_skew() on different parts of the genome
We traverse the genome with several windows of fixed size
Each window starts after the end of the previous one
In other words, the windows do not overlap
Create a vector with the window’s positions
We start at the first DNA position, until the last
Be careful to not step out of DNA
win_pos <- seq(from=1, to=length(dna)-size, by=size)
Now we apply gc_skew() to each element of win_pos
The result depends on window’s size
Result for size=1E5

Result for size=1E4

Result for size=1E3

Result for size=1E2

Finding replication origin using GC skew
The relation between %G and %C is not constant over all the genome
In some genome regions there are more G than C
We can evaluate this using the GC skew \[\frac{G-C}{G+C}\]
DNA replication
There is a richness of G over C and T over A in the leading strand
(and vice versa for the lagging strand)
GC skew changes sign at the boundaries of the two replichores
This corresponds to DNA replication origin or terminus
DNA replication
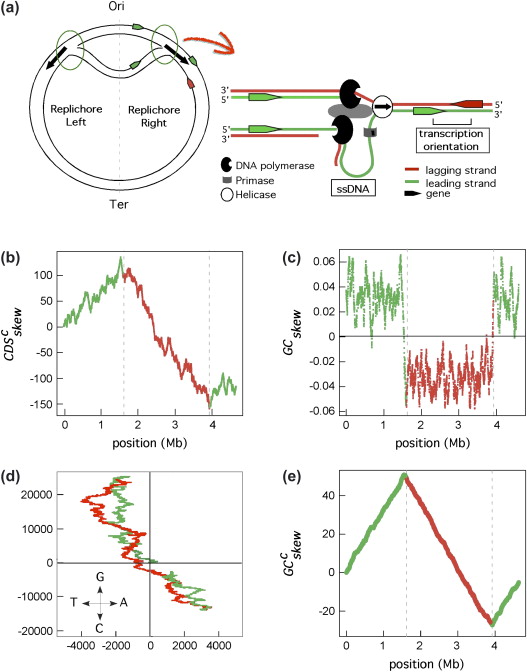
Marie Touchon, Eduardo P.C. Rocha, (2008), From GC skews to wavelets: A gentle guide to the analysis of compositional asymmetries in genomic data,
Biochimie, Volume 90, Issue 4,
Video
Finding the origin
- The GC skew is positive in one part of chromosome
- And negative on the other, on average
- It changes sign in two places
The reason for this asymmetry is the DNA replication process
The origin of replication is in one of the sign changing places
How can we find the change of sign
We want to write a program so we can find Ori on many different genomes
We can answer questions like:
- Are both replichores of the same size?
- If they are different, what is the biological reason?
- Is there some insertion?
- What are the extra genes? What do they do?
Finding the change of sign is not so easy
The values can change a lot between a window and the next one
skew data is noisy. A lot of small random changes
There is an easier way to find Ori
Instead of looking directly at skew, we can look at accumulative skew
\[\text{acc_skew}[i]=\text{skew}[i]+\text{skew}[i-1]+\cdots+\text{skew}[1]\]
Now, instead of the change of sign, we look for the minimum and maximum (Why?)
Now it is easier to see the change of sign

The dictionary says
- accumulative
- § (adjective) increasing in quantity, degree, or force by successive additions.
- § increasing, accumulative, growing, mounting; collective, aggregate, amassed.
- § the accumulative effect of two years of drought
- § the effects of pollution are accumulative
Accumulative sum
Everyday you spend some money
Some days you receive money
How much money you have each day?
Accumulative Sum: daily balance
The income can be positive (salary) or negative (expenses)
The balance on first day is your initial money
The balance of today is the balance of yesterday plus the income of today
balance[today] <- balance[yesterday] + income[today]
balance and income are vectors
Since they have different values every day, we represent the income on day i by income[i]
We also represent the balance on day i by balance[i]
The vector income has the values for all days
The element income[i] has the value for a single day
Today and yesterday
We will see several “days”, represented by i
It is useful to think that
irepresents “today”i-1represents “yesterday”
If we know income, we can calculate balance
The balance on first day is your initial money
balance[1] <- income[1]
The balance of today is the balance of yesterday plus the income of today
for(i in 2:length(income)) {
balance[i] <- balance[i-1] + income[i]
}
Balance looks like this
The same idea applies to GC-skew
The GC skew in each window is like the income in each day
And we want to see the “balance”: accumulative skew
acc_skew[1] <- skew[1]
for(i in 2:length(skew)) {
acc_skew[i] <- acc_skew[i-1] + skew[i]
}
Same pattern, same solution
Can you write this as a function?
Now max & min show the change of sign

Position of the maximum
The maximum value of acc_skew is
max(acc_skew)
[1] 4.9877
It is not really important
We are looking for position, not value of maximum
Position of the maximum
This is the index of the maximum in the acc_skew vector
which.max(acc_skew)
[1] 155
This is always an integer number, between 1 and length(acc_skew)
It is not the position in the genome
Position of the maximum
Since acc_skew vector has the same size as win_pos, we can find the Ori position with this
win_pos[which.max(acc_skew)]
[1] 1540001
win_pos contains the genome positions of each window
This code gives us the position of the window with maximum GC-skew
Locating origin depends on window size
Ori is located in the interval between
win_pos[which.max(acc_skew)]win_pos[which.max(acc_skew)] + size
Skew and Accumulative skew
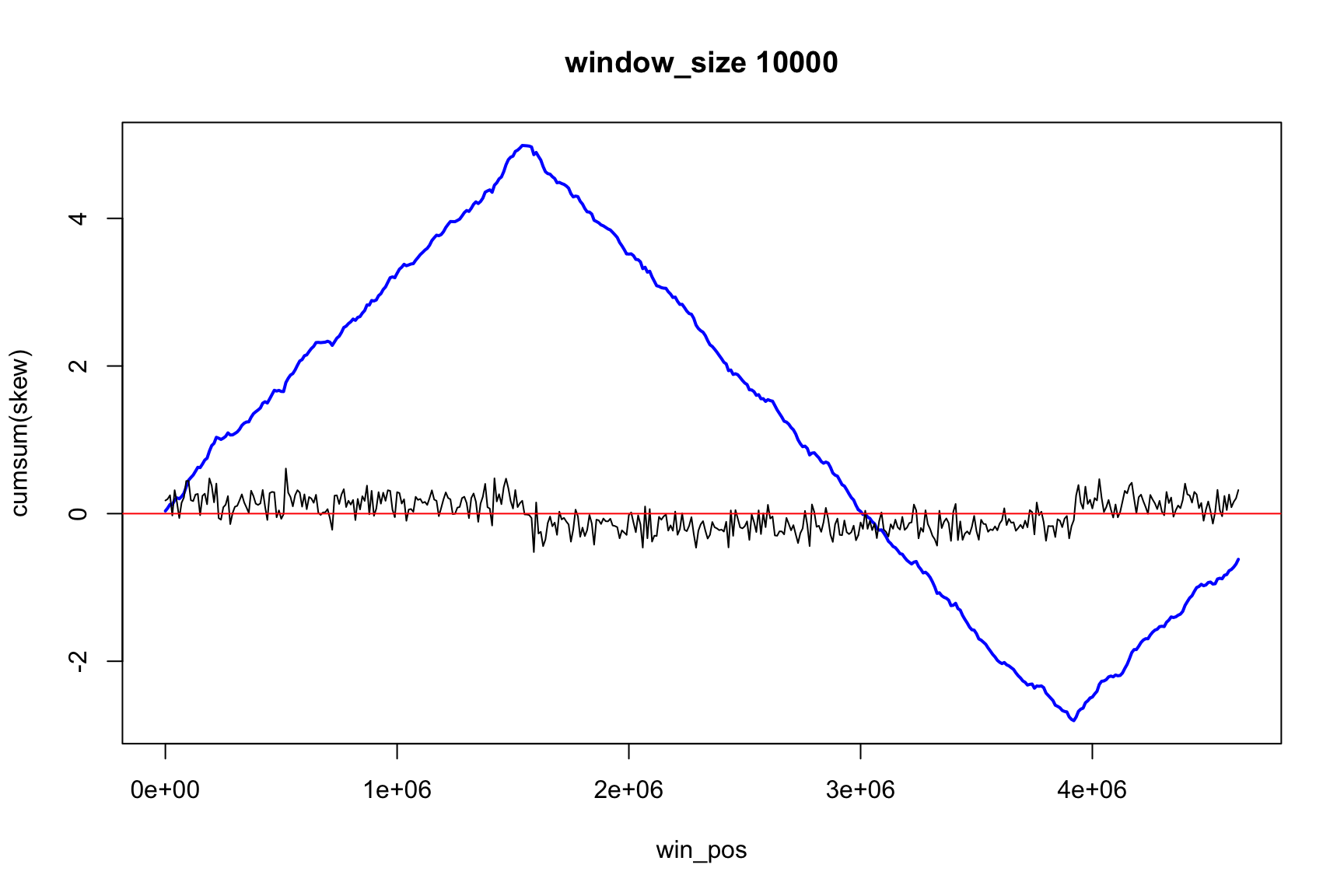
Skew and Accumulative skew
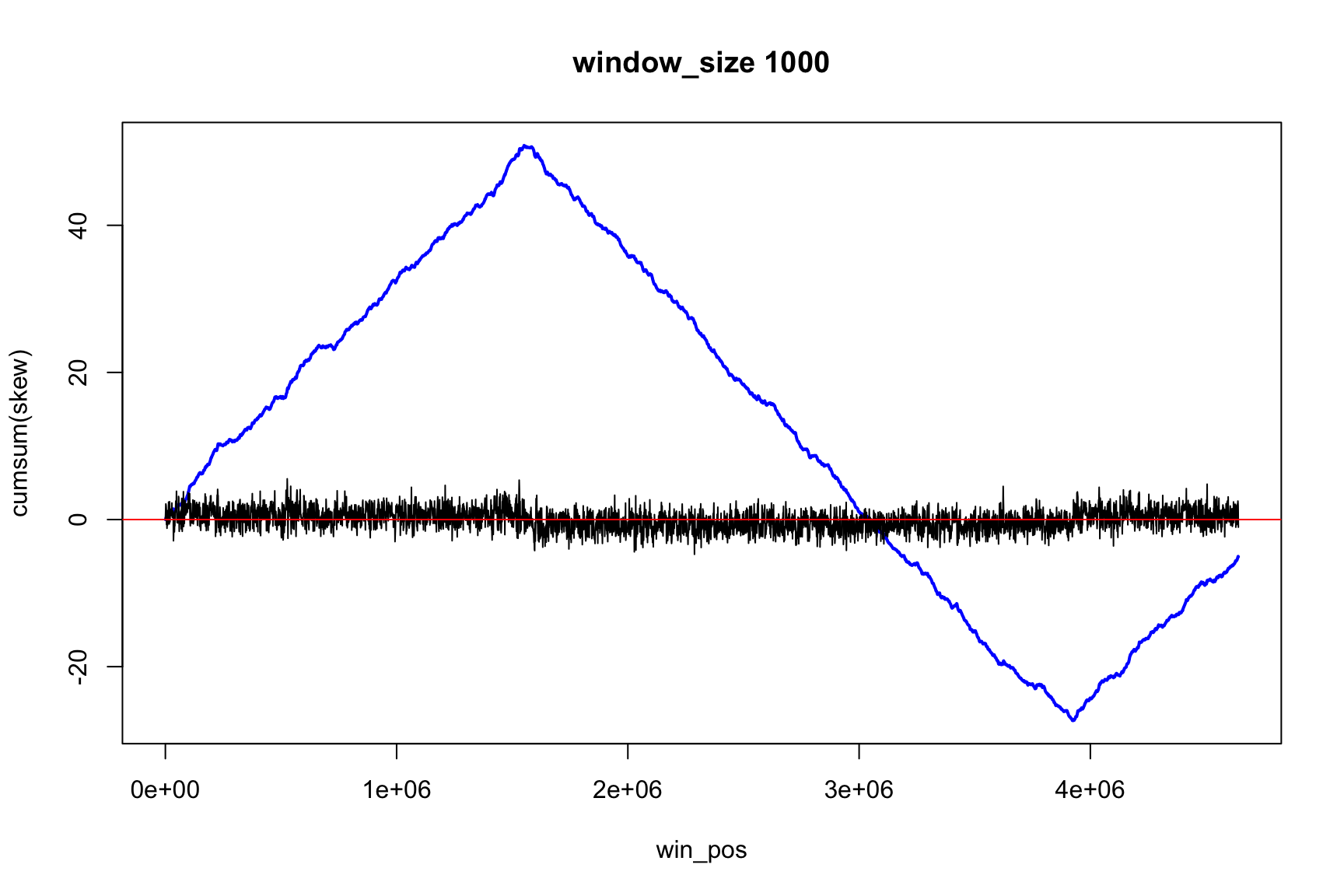
Skew and Accumulative skew
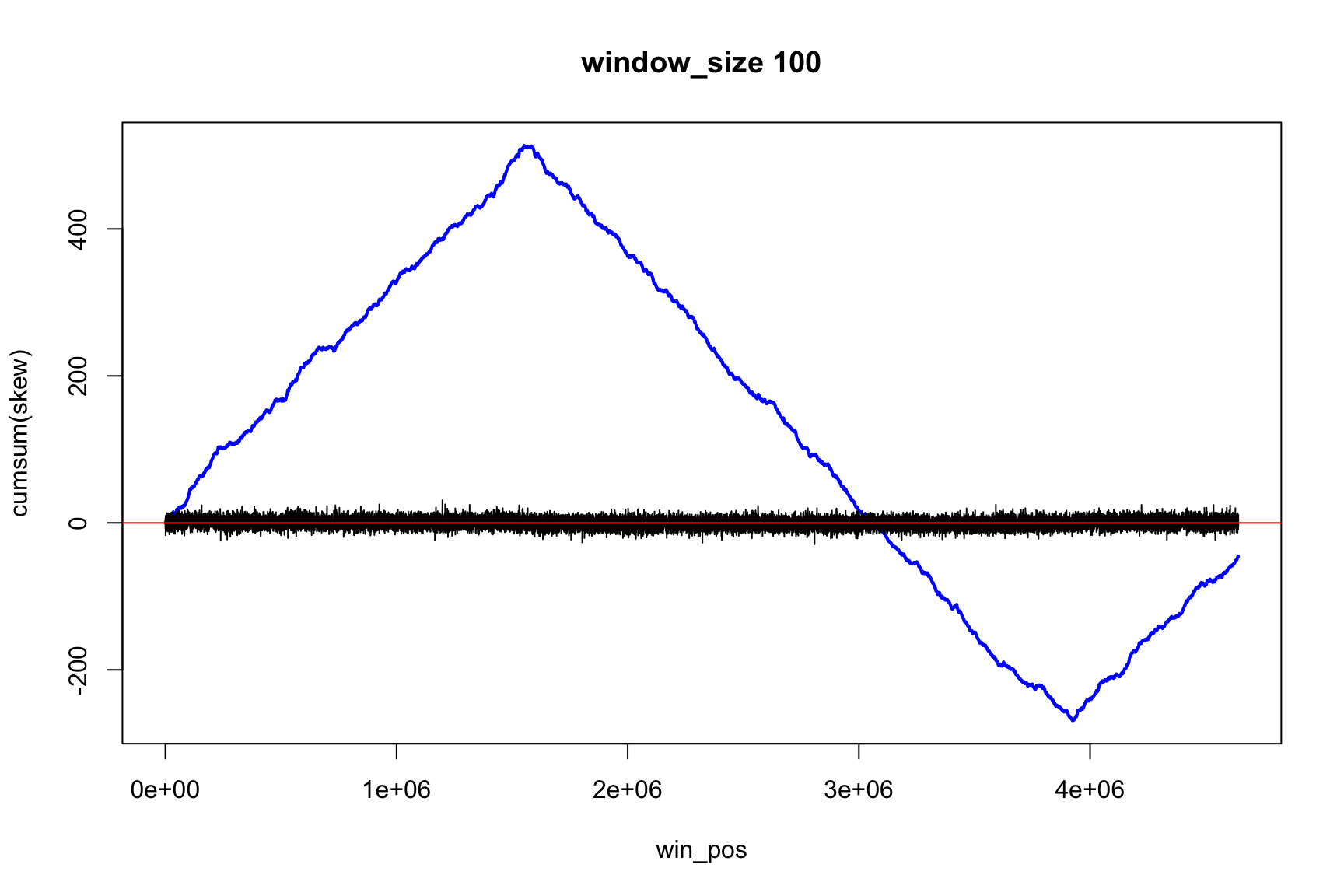
Skew and Accumulative skew
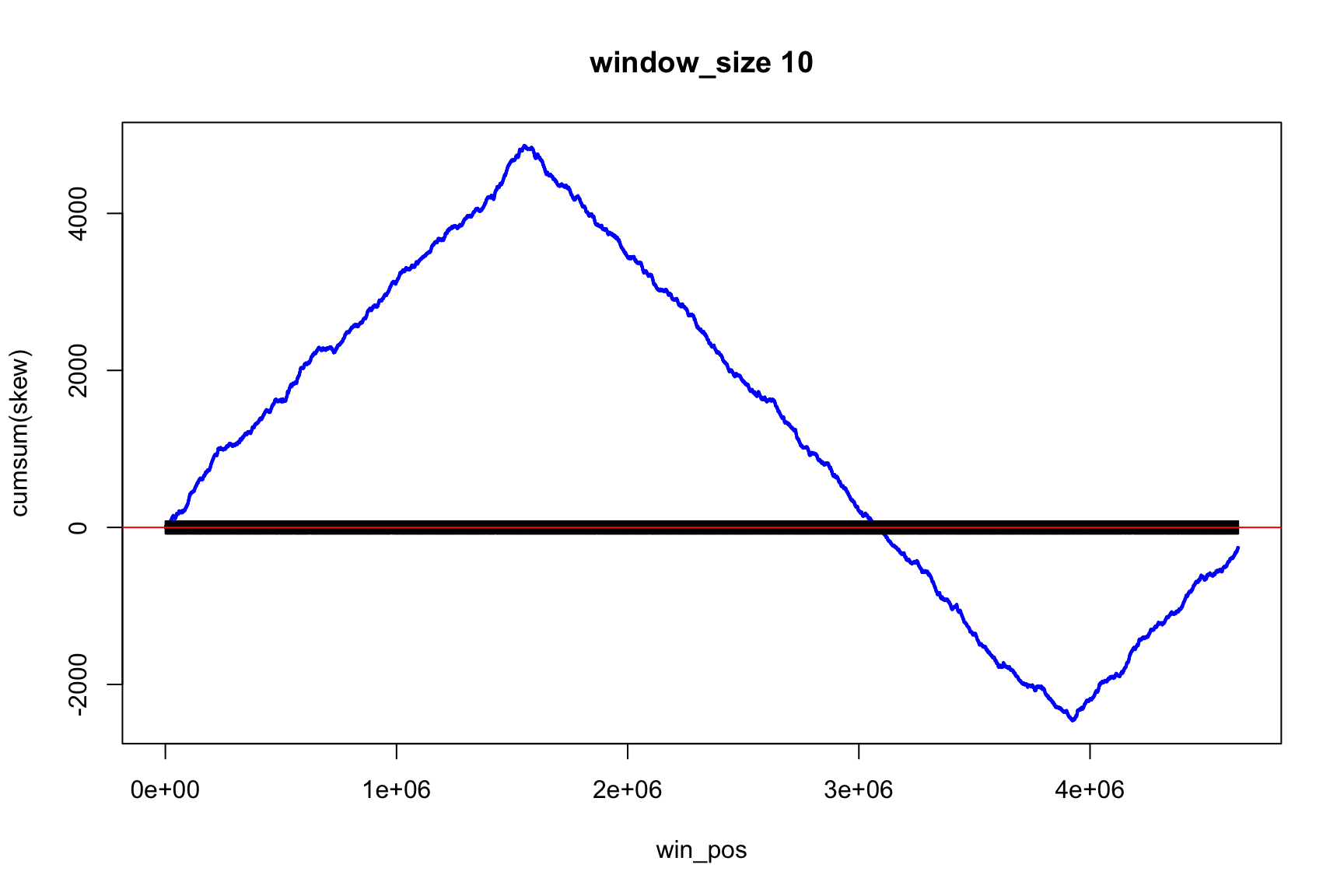
skew changes fast, acc_skew changes slow
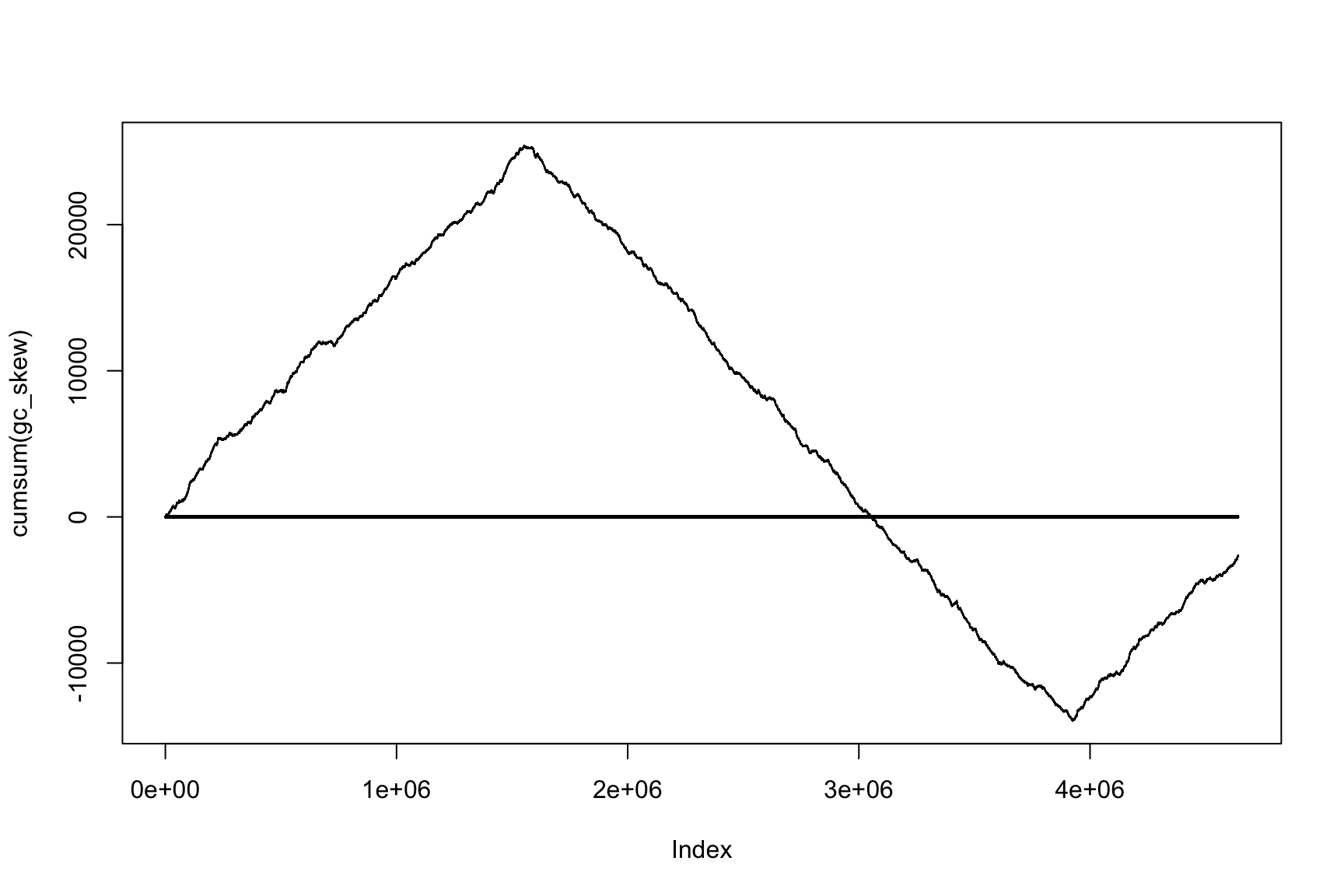
Accumulative sums are useful
- If we know the income, we can get balance
- If we know the skew, we can get acc_skew
- If we know the change, we can know the state