Class 9: Multiple Sequence Alignment
Bioinformatics
Andrés Aravena
27 November 2020
Multiple sequence alignment
Why?
- to study closely related genes or proteins
- to find conserved domains
- to find the evolutionary relationships
- the base of phylogenetic trees
- to identify shared patterns among related genes
- conserved sequences can be binding sites
In the previous chapter…
We discussed pairwise alignment
- Global, using Needleman & Wunsch algorithm
- also for semi-global alignment
- Local, using Smith & Waterman algorithm
Both methods use a dot-plot matrix
We build a matrix with \(m\) rows and \(n\) columns
The cost (in time and memory) is \[O(mn)\]
(\(m\) is the query length, \(n\) is the subject length)
BLAST is for database search
If there are \(d\) entries in the database, a direct search will have a cost \[O(mnd)\] where \(n\) is the average subject length
BLAST improves the search using an index to find “seeds”
Then BLAST builds a dot-plot matrix around the “seed”
Filling the dot-plot matrix
To find the optimal alignment, we look for diagonals in the matrix that maximize the total score
Every cell \(M_{ij}\) in the matrix has initially the value \[M_{ij}=Score_2(s_{1}(i),s_{2}(j))\] where \(s_{1}(i)\) is the letter in position \(i\) of sequence \(s_1\),
and \(s_{2}(j)\) is the letter in position \(j\) of \(s_2\)
Pairwise to three-wise alignment
To aligning two sequences, we build a dot-plot matrix.
That is, a rectangle.
To align three sequences, we need a three-dimensional array.
That is, a cube.
Each cell \(M_{ijk}\) has value \[M_{ijk}=Score_3(s_{1}(i),s_{2}(j), s_{3}(k))\]
Cost of three-wise alignment
If the three sequences have length \(m_1, m_2,\) and \(m_3,\) then building the cube has cost \[O(m_1\cdot m_2\cdot m_3)\]
To simplify, we assume that all sequences have length \(m\)
Then the cost of three-wise alignment is \[O(m^3)\]
Multiple alignment
Following the same idea…
To align \(N\) sequences, we need a dot-plot in \(N\) dimensions.
\[M_{i_1,\ldots,i_N}=Score_N(s_{1}(i_1),s_{2}(i_2),…,s_{N}(i_N))\]
Therefore, if the average sequence length is \(m,\) then the cost is \[O(m^N)\]
How much is that?
To fix ideas, assume that \(m=1000\)
Therefore the cost is \[O(1000^N)=O(10^{3N})\]
How many seconds
Now assume that the computer can do one million comparisons each second
The number of seconds is then \[O(10^{3N-6})\]
How much is that?
Under these hypothesis we have this table
| \(N\) | Seconds |
|---|---|
| 2 | \(10^0\) |
| 4 | \(10^6\) |
| 8 | \(10^{18}\) |
| 12 | \(10^{30}\) |
Exercise
Translate these numbers to days, years, etc.
How do these numbers change if \(m\) changes?
What happens if the computers are 1000 times faster?
What is the largest multiple alignment that you can do in your life?
What is the largest number of sequences that can be aligned?
What can we do to align more sequences?
Write your answers in the Quiz
Heuristic
This is clearly too expensive, so we need heuristics
(i.e. solving a similar but simpler problem)
One common idea is to do a progressive alignment
- start with a pairwise alignment,
- and then align the rest one by one
Too many heuristics
There are several ways to simplify the original problem
Thus, there are many approximate solutions
The main differences are:
- How to decide what to align first?
- Can new sequences change the previous alignment?
- Can \(s_k\) change the alignment of \((s_1,…,s_{k-1})\)?
- How to use additional information (like 3D structure)?
- What is the formula for \(Score_k(s_{1}(i_1),…,s_{k}(i_k))\)?
Some common Multiple-Alignment tools
- Clustal
- ClustalW, ClustalX, Clustal Omega
- T-Coffee
- 3D-Coffee
- MUSCLE
- MAFFT
Clustal
Clustal Omega
Clustal was the first popular multiple sequence aligner
Versions: Clustal 1, Clustal 2, Clustal 3, Clustal 4, Clustal V, Clustal W, Clustal X, Clustal Ω
Only the last is currently in use
Clustal W
This version is easier to explain
Scoring function
First, there should be a scoring function
Clustal uses a simple one. The sum of all v/s all \[\begin{aligned} Score_k(s_{1}(i_1),…,s_{k}(i_k))= & Score_2(s_{1}(i_1),s_{2}(i_2)) + \\ & Score_2(s_{1}(i_1),s_{3}(i_3)) + \cdots+ \\ & Score_2(s_{k-1,i_{k-1}},s_{k}(i_k)) \end{aligned} \] where \(Score_2(s_{a}(i),s_{b}(j))\) is PAM, BLOSUM, or a suitable substitution scoring matrix
Progressive alignment order
We start by comparing sequences all-to-all
That is, comparing all pairs of sequences
We store them in a distance matrix
How many pairs can be done with \(N\) sequences?
Building a guide tree
Once we get all pairwise “distances”
(that is, scores)
We make a tree by hierarchical clustering
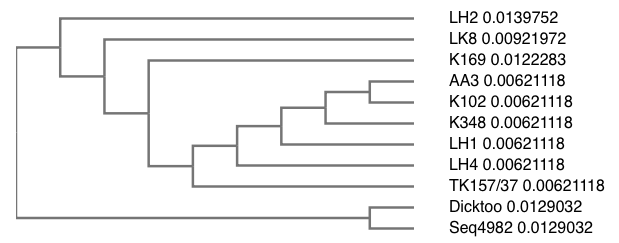
Hierarchical clustering
Start with one leaf node for each sequence, and no branches
- Take the two sequences (\(A\) and \(B\)) that are more similar (highest score)
- create a new node \(C\) connected to \(A\) and \(B\)
- \(Score_2(X,C)\) between each old node \(X\) and \(C\) is the average of \(Score_2(X,A)\) and \(Score_2(X,B)\) \[Score_2(X,C)=\frac{Score_2(X,A)+Score_2(X,B)}{2}\]
- forget about \(A\) and \(B\)
This is not a phylogenetic tree
The guide tree is built without seeing the big picture
So it is not safe to assign any meaning to it
We will talk more about trees and build phylogenetic trees later
Guide tree guides the alignment

Clustal aligns the sequences following the guide tree
First, it aligns the more similar sequences
Then it adds the nearest sequence, and so on
These are semi-global alignments
Uses \(Score_k()\) when there are \(k\) sequences
Practice
Search for CLUSTAL
Solving without aligning
Motifs
Short patterns, usually without gaps
- Binding sites in DNA
- Active sites in proteins
Sometimes they can be found with experiments like ChIP-seq
Finding motifs characteristics
If we know several instances of binding sites, we can align them
After we align them, we can calculate the frequency of each symbol on each column
If we know these frequencies, we can build a position specific score matrix
These PSSM represent the motif
Finding new motif instances
If we know the PSSM, it is easy to find new sites matching the motif
We just use the PSSM to give a score to each symbol, and we get a total score.
High scores will be new motif instances
How to find motifs without alignment

It is easy to prepare PSSM in a multiple alignment
But we have seen that multiple alignment can be expensive
When we are looking for short patterns (a.k.a motifs) we can use other strategies
Nucleic Acids Research, Volume 34, Issue 11, 1 January 2006, Pages 3267–3278, https://doi.org/10.1093/nar/gkl429
Formalization
Given \(N\) sequences of length \(m\): \(s_1, s_2, ..., s_N\), and a fixed motif width \(k,\) we want
- a subsequence of size \(k\) (a \(k\)-mer) that is over-represented among the \(N\) sequences
- or a set of highly similar \(k\)-mers that are over-represented
Testing all sets of \(k\)-mers is computationally intensive, so several heuristics have been proposed
Gibbs Sampling Algorithm
Given \(N\) sequences of length \(m\) and desired motif width \(k\):
Step 1: Choose a position in each sequence at random: \[a_1 \in s_1, a_2 \in s_2, ..., a_N \in s_N\]
Step 2: Choose a sequence at random from the set (let’s say, \(s_j\)).
Step 3: Make a PSSM of width \(k\) from the sites in all sequences except \(s_j.\)
Gibbs Sampling Algorithm (cont)
Step 4: Assign a score to each position in \(s_j\) using the PSSM constructed in step 3: \[p_1, p_2, p_3, ..., p_{m-k+1}\]
Step 5: Choose a starting position in \(s_j\) (higher score have higher probability) and set \(a_j\) to this new position.
Gibbs Sampling Algorithm (cont)
Step 6: Choose a sequence at random from the set (say, \(s_{j'}\)).
Step 7: Make a PSSM of width \(k\) from the sites in all sequences except \(s_{j'}\), but including \(a_j\) in \(s_j\)
Step 8: Repeat until convergence (of positions or motif model)
Step 1
Choose a position \(a_i\) in each sequence at random 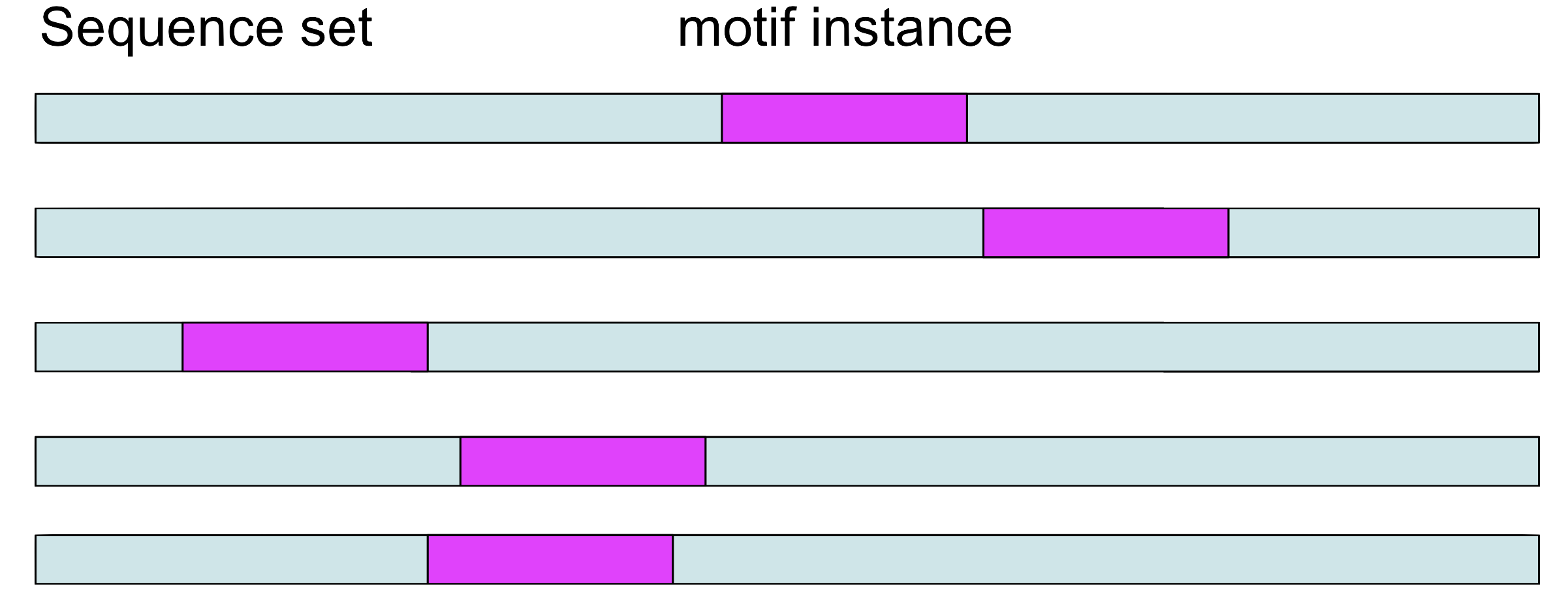
Step 2 and 3
Choose a sequence at random, let’s say \(s_1.\) Make a PSSM from the sites in all sequences except \(s_1\) 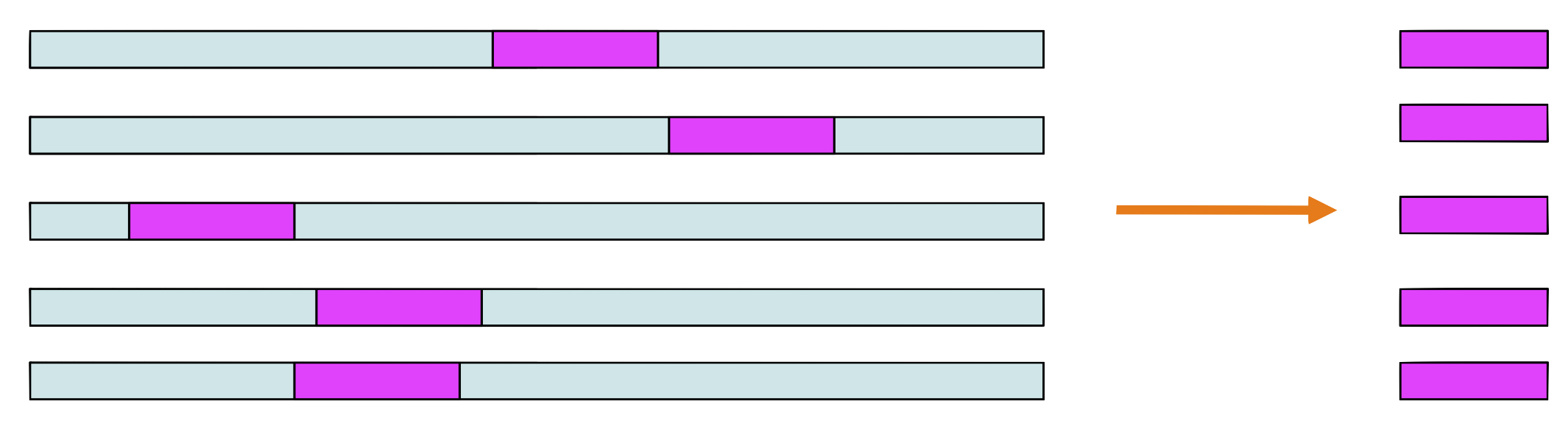
Step 4
Assign a score to each position in using the PSSM
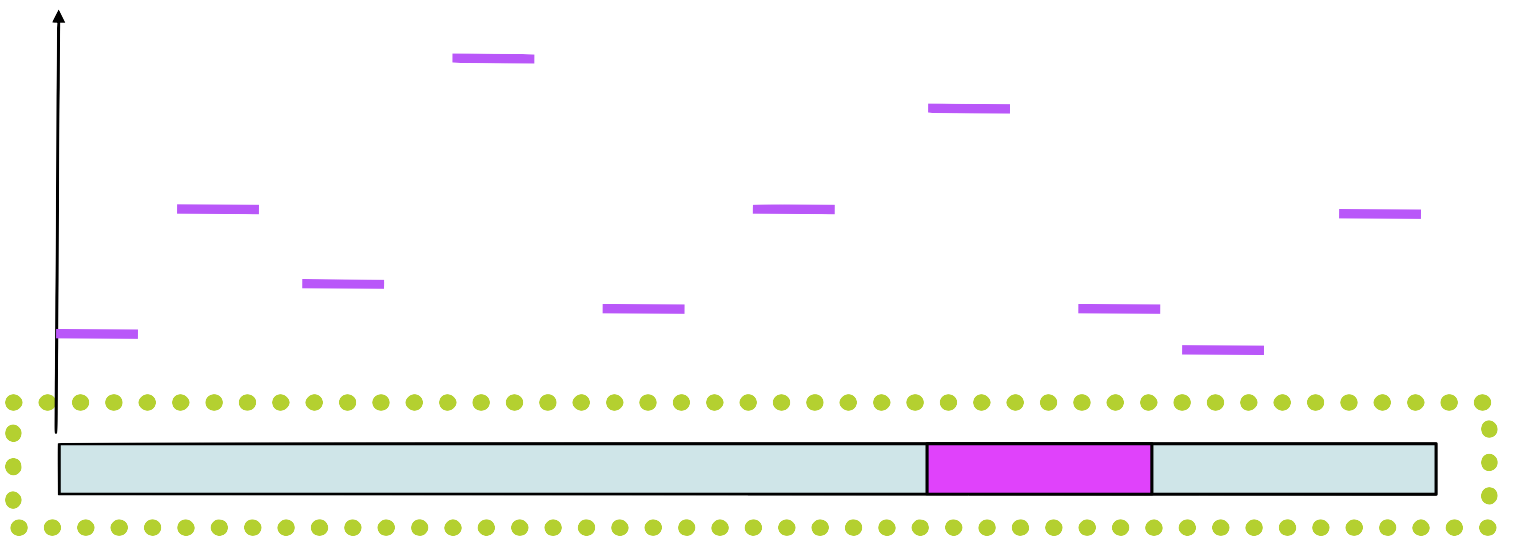
Step 5
Choose a new position in \(s_1\) based on this score 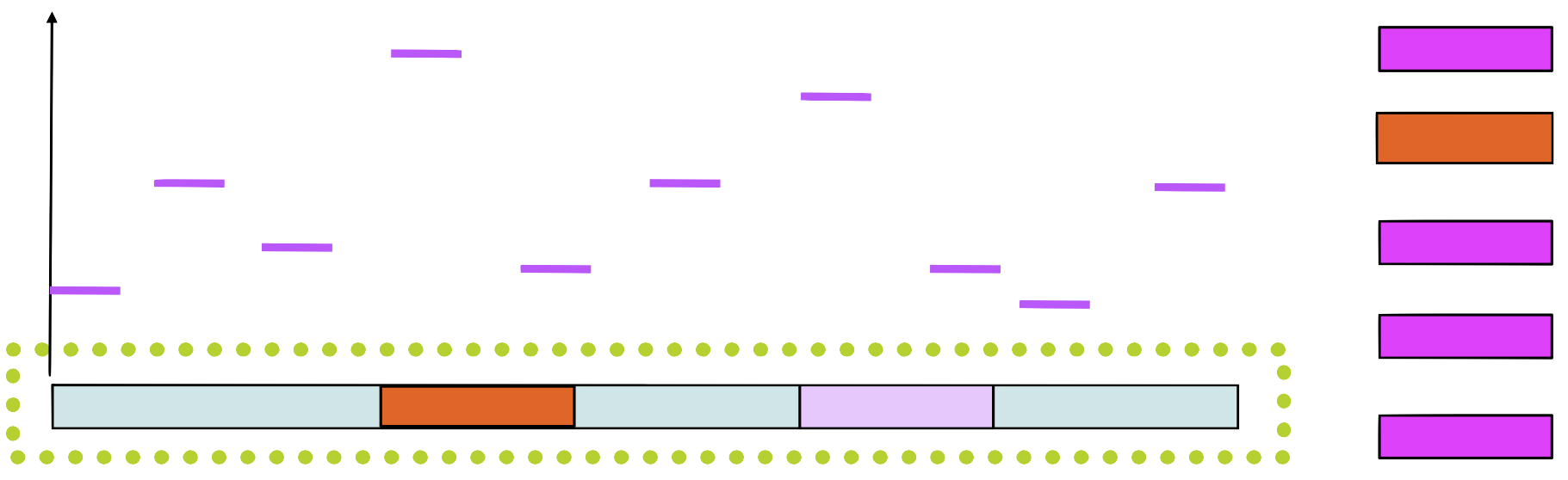
Step 6
Build a new PSSM with the new sequence 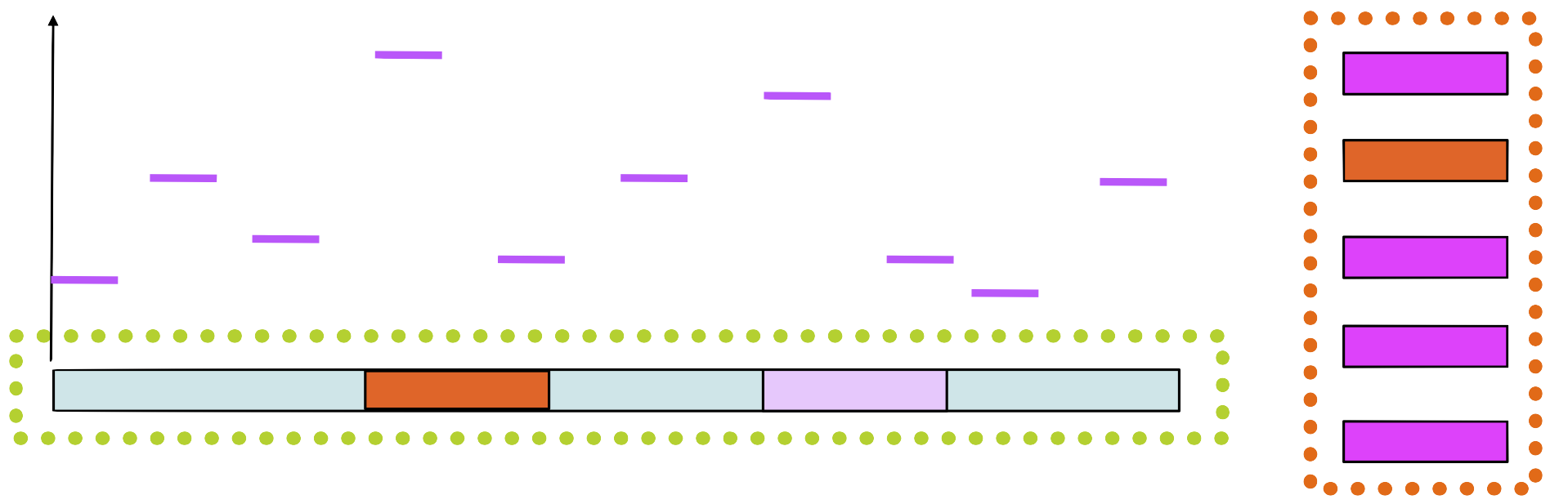
Step 7
Choose randomly a new sequence from the set and repeat 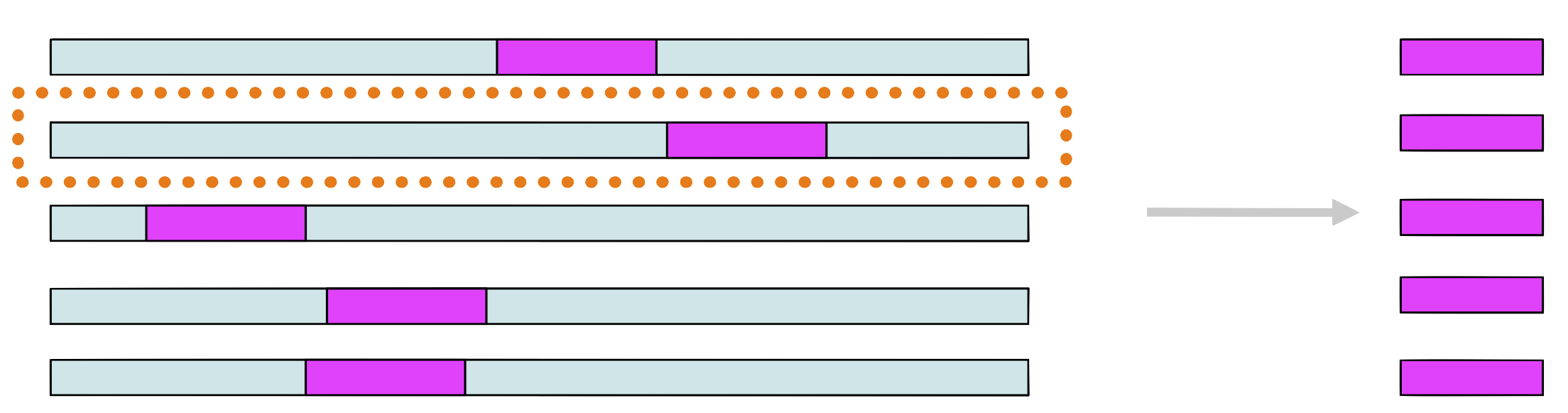
Convergence
We repeat the steps until the PSSM no longer changes
Alternative: we stop when the positions \(a_i\) do not change
The methods probably gives us a over-represented motif
Implementation
- Gibbs Motif Sampler Homepage: http://ccmbweb.ccv.brown.edu/gibbs/gibbs.html
- MotifSuite: http://bioinformatics.intec.ugent.be/MotifSuite/Index.htm
- MEME on the MEME/MAST suite