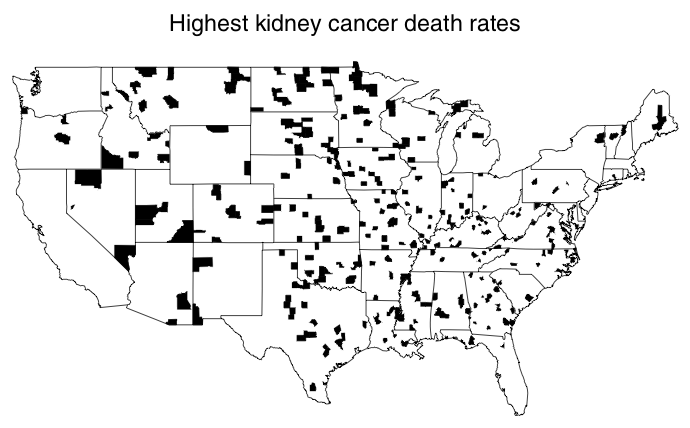
Highest kidney cancer rates in US (1980–1989) were in rural areas
May 3rd, 2019
Where are the cancers?
Highest rates of kidney cancer are in rural areas
Why? Maybe…
- the health care there is worse than in major cities
- High stress due to poverty
- are exposed to more harmful chemicals
- Drink Alcohol
- Smoke Tobacco
Lowest rates of kidney cancer are in rural areas
Why? Maybe…
- No air and water pollution.
- No stress
- Eat healthy foods
Something is wrong, of course. The rural lifestyle cannot explain both very high and very low incidence of kidney cancer.
Why smaller genes have extreme GC content
Remember some concepts
- Random variable
- number that depends on the outcome of a random process
- Average of population
- a fixed number, that we do not know and want to know
- Average of a sample
- a random variable, that we get from an experiment
Many things are averages
- concentration
- proportion
- density
- GC content
- frequency of events
What is the relationship between sample average and population average?
Can we learn the population average from the sample average?
Example: cell counting
Hemocytometer
Each square is a sample. Volume is fixed. The cell count is an average of cell counts of some squares.
We want population cell density
We have a sample of cell densities
Different samples have different average
N <- 4800 pop_LD <- sample(rep(0:9,N/10)) pop_MD <- sample(rep(0:29,N/30)) pop_HD <- sample(rep(0:79,N/80)) pop_HD
[1] 64 77 47 76 43 17 0 47 6 14 28 46 69 18 43 17 [17] 8 6 13 44 58 21 8 3 31 36 75 74 57 12 14 0 [33] 72 21 23 56 37 6 79 14 0 27 22 34 22 53 76 65 [49] 7 72 25 32 59 61 6 77 61 58 66 19 59 67 49 40 [65] 36 35 15 69 47 72 63 38 70 36 77 53 56 66 21 46 [81] 64 24 76 42 66 41 55 49 69 71 1 1 38 68 33 71 [97] 1 16 77 57 50 62 15 62 4 19 28 57 73 7 62 3 [113] 52 9 20 43 47 54 77 58 4 33 27 12 44 60 23 35 [129] 21 68 16 49 65 63 65 59 46 29 42 6 34 18 70 68 [145] 54 32 73 57 23 18 61 20 39 54 77 54 76 71 72 20 [161] 47 53 73 31 2 12 34 7 18 76 53 50 24 4 36 16 [177] 37 40 18 27 47 31 7 18 36 38 63 9 19 1 51 67 [193] 29 54 27 56 75 64 37 21 73 56 31 12 36 76 75 63 [209] 73 63 66 50 29 33 65 23 63 53 61 20 23 55 30 0 [225] 10 8 20 1 61 70 53 45 3 41 49 48 59 68 55 77 [241] 74 72 2 35 65 51 71 7 54 62 67 31 72 28 20 64 [257] 55 4 56 16 67 14 13 57 60 32 36 39 74 75 76 24 [273] 16 76 69 21 66 14 60 54 19 48 36 66 47 32 3 64 [289] 25 14 59 6 57 40 39 79 72 1 47 64 18 42 31 38 [305] 13 42 16 75 68 32 7 61 23 18 74 39 73 7 0 53 [321] 69 40 50 75 70 77 28 71 55 42 15 72 78 14 26 47 [337] 49 55 77 65 77 14 73 21 60 76 53 16 38 35 75 55 [353] 46 16 51 73 65 27 6 39 66 39 7 54 4 76 23 79 [369] 7 48 3 16 21 24 61 54 75 41 29 1 78 13 0 48 [385] 22 70 33 31 18 2 71 6 18 42 60 54 38 19 34 43 [401] 6 67 67 5 72 45 9 4 2 15 51 69 27 15 66 54 [417] 75 62 2 54 75 42 66 71 55 4 77 20 76 50 13 47 [433] 46 53 9 34 26 59 34 20 22 46 23 65 0 39 42 36 [449] 11 36 10 34 37 26 66 30 55 48 38 8 64 34 28 43 [465] 17 61 37 7 11 47 26 48 43 30 33 3 1 68 72 15 [481] 72 28 66 10 34 58 56 27 47 17 45 17 38 51 40 49 [497] 19 67 73 35 18 73 68 28 11 29 53 22 65 45 26 33 [513] 61 2 7 14 60 8 15 48 56 59 35 44 52 59 44 24 [529] 77 33 59 41 52 5 23 66 61 15 64 65 52 62 13 4 [545] 53 73 46 77 43 9 43 32 35 76 10 29 44 29 27 54 [561] 30 62 48 46 63 72 0 10 58 42 12 73 52 47 38 6 [577] 77 44 23 27 60 65 6 41 62 58 52 6 66 11 78 25 [593] 17 48 64 43 23 42 37 48 40 57 22 33 6 38 71 25 [609] 1 46 20 7 42 70 21 15 38 54 79 72 54 3 78 60 [625] 52 8 50 48 70 4 43 59 38 38 78 7 12 29 45 12 [641] 29 19 18 15 38 52 50 13 38 24 47 49 34 72 73 67 [657] 8 6 12 59 76 76 10 21 70 58 14 46 54 14 16 79 [673] 60 64 45 2 32 46 42 74 68 72 74 26 79 43 8 14 [689] 4 54 52 27 29 33 48 68 77 64 46 55 33 68 57 25 [705] 72 12 58 60 44 68 7 79 5 62 55 49 46 29 57 18 [721] 5 42 33 68 25 0 35 29 47 51 11 14 12 20 50 77 [737] 19 30 64 52 58 59 30 65 4 44 60 70 6 12 74 31 [753] 27 52 1 55 27 14 32 23 71 10 73 33 1 67 59 15 [769] 62 40 7 18 48 69 22 55 75 52 32 62 44 78 70 0 [785] 62 13 77 9 66 78 24 8 74 68 65 27 77 48 12 2 [801] 68 72 56 72 12 23 42 22 70 78 26 54 57 71 15 1 [817] 3 1 9 59 51 14 12 61 35 49 16 51 26 78 10 52 [833] 30 6 40 21 31 30 23 19 53 3 18 28 36 8 78 16 [849] 63 75 51 32 76 3 15 29 61 79 33 20 63 28 56 22 [865] 35 24 64 18 20 63 13 39 15 31 33 26 43 2 55 63 [881] 24 41 20 25 6 0 53 67 71 14 3 30 22 19 68 24 [897] 37 14 12 18 74 39 51 24 42 49 64 53 20 32 62 58 [913] 53 50 48 63 22 64 69 77 52 62 7 45 13 12 68 36 [929] 54 20 26 45 21 25 78 56 19 50 69 9 37 42 8 16 [945] 62 75 62 20 9 71 20 45 9 42 31 58 35 69 21 34 [961] 62 52 6 37 65 10 16 2 68 72 24 47 26 72 63 75 [977] 49 15 40 13 29 41 79 50 50 20 79 24 25 2 49 60 [993] 73 18 31 7 51 45 20 69 44 40 51 64 64 28 44 5 [1009] 19 19 78 54 45 52 29 36 61 51 48 32 77 6 68 77 [1025] 74 42 21 67 65 29 62 70 56 61 20 16 66 58 71 69 [1041] 48 60 17 35 13 14 18 19 8 25 49 47 12 18 1 62 [1057] 26 17 76 56 45 48 76 48 66 55 39 53 31 26 43 61 [1073] 2 52 59 16 5 59 31 17 2 10 72 72 61 3 62 54 [1089] 38 53 35 3 56 77 9 71 28 18 79 12 12 31 11 74 [1105] 33 71 28 4 37 48 41 28 79 32 9 68 14 36 49 71 [1121] 30 55 63 9 51 25 44 2 9 27 60 5 71 3 18 8 [1137] 75 69 51 44 16 12 69 8 23 21 8 53 20 53 25 1 [1153] 14 10 73 42 11 32 54 75 12 41 32 44 47 15 27 30 [1169] 10 44 31 39 30 35 61 57 26 34 14 24 52 9 53 7 [1185] 13 66 49 14 43 34 40 71 60 19 49 77 37 60 58 67 [1201] 22 15 2 25 34 77 55 30 49 63 61 13 21 29 53 14 [1217] 1 64 64 59 33 57 59 44 35 19 57 4 33 14 34 43 [1233] 58 36 20 29 78 26 13 39 0 7 70 79 43 77 59 23 [1249] 17 21 52 58 73 79 15 66 37 56 6 45 56 40 7 79 [1265] 77 8 9 6 38 68 71 45 0 2 8 46 57 63 32 46 [1281] 49 33 39 33 40 30 3 18 23 0 60 19 31 64 62 54 [1297] 29 44 15 64 52 72 3 0 13 43 73 50 25 6 57 70 [1313] 42 16 77 9 56 52 67 75 55 73 77 65 47 9 51 11 [1329] 68 52 69 77 67 78 0 74 53 49 31 10 23 47 69 71 [1345] 46 34 74 67 68 58 41 46 21 30 37 46 60 38 37 45 [1361] 18 23 73 79 44 12 54 7 77 47 19 39 72 22 11 44 [1377] 13 46 77 9 71 79 14 74 23 46 67 46 35 67 9 40 [1393] 56 11 6 30 1 53 68 70 57 44 61 36 59 43 11 23 [1409] 60 21 1 58 59 3 78 11 14 2 62 35 70 37 64 65 [1425] 22 34 65 16 8 2 39 15 57 68 79 36 38 72 52 63 [1441] 13 16 20 7 70 68 32 12 8 12 47 54 61 40 10 41 [1457] 21 67 38 28 70 24 55 44 56 69 45 59 28 73 35 31 [1473] 6 57 38 22 19 44 16 79 67 48 45 18 7 44 78 72 [1489] 32 44 35 13 54 66 72 72 4 70 15 67 69 40 37 45 [1505] 43 76 0 44 28 6 19 30 19 45 30 51 68 4 22 35 [1521] 70 47 6 55 43 50 49 75 1 23 24 19 32 42 49 59 [1537] 59 75 59 46 49 2 29 21 42 28 50 10 36 50 21 70 [1553] 67 20 51 78 11 65 7 10 66 7 19 36 30 18 77 24 [1569] 44 59 25 47 12 44 40 54 63 47 68 71 79 38 35 63 [1585] 4 17 49 45 65 78 15 67 41 13 57 3 21 29 0 41 [1601] 29 48 4 71 5 31 77 36 30 41 35 31 74 31 42 73 [1617] 12 44 15 17 44 5 63 4 60 1 54 65 33 77 64 12 [1633] 3 16 4 52 69 25 57 17 9 51 48 70 55 37 14 15 [1649] 14 17 59 25 49 57 8 33 41 61 52 43 22 0 55 76 [1665] 71 26 49 40 53 41 25 61 22 28 26 27 65 67 41 15 [1681] 78 59 37 29 76 41 48 71 47 44 47 24 77 34 71 7 [1697] 28 55 43 12 26 10 66 50 38 53 58 65 40 34 0 8 [1713] 59 11 23 61 57 17 15 20 50 0 63 6 38 8 60 37 [1729] 28 35 59 35 8 10 24 5 66 58 3 13 61 2 21 30 [1745] 64 74 78 67 0 35 21 8 16 20 31 5 1 58 53 8 [1761] 29 51 4 2 16 58 47 61 34 73 11 52 40 28 49 21 [1777] 65 75 54 4 13 50 25 26 49 18 55 56 14 39 12 16 [1793] 34 9 57 20 68 9 40 28 56 65 38 4 76 0 0 56 [1809] 22 51 5 68 1 11 36 75 51 79 64 7 4 37 69 43 [1825] 4 39 44 9 54 75 35 64 24 34 59 60 7 3 79 48 [1841] 29 12 0 32 65 59 62 55 73 65 7 70 10 25 32 13 [1857] 36 3 47 44 62 23 1 13 51 42 25 79 19 71 24 11 [1873] 65 37 67 13 46 69 32 79 9 19 22 40 62 48 32 74 [1889] 22 23 53 40 0 51 2 73 69 18 50 57 45 55 26 52 [1905] 20 2 62 79 24 22 14 51 79 28 8 74 8 5 64 1 [1921] 60 56 73 70 7 58 44 62 22 40 52 18 68 24 2 64 [1937] 43 20 72 20 71 70 25 37 46 42 65 54 1 7 43 56 [1953] 14 43 38 64 29 34 74 55 37 39 42 38 61 23 18 60 [1969] 29 4 56 27 47 35 45 38 0 4 21 60 74 10 59 42 [1985] 17 51 49 39 58 74 39 77 0 65 79 16 36 79 25 3 [2001] 35 5 52 47 70 13 31 65 69 20 71 25 49 27 1 25 [2017] 57 29 41 56 16 63 56 9 24 41 17 43 6 26 48 23 [2033] 19 72 53 66 44 59 32 57 3 11 72 39 29 3 52 36 [2049] 19 39 63 11 41 41 66 26 73 8 10 24 40 8 60 76 [2065] 35 12 19 75 42 44 61 52 1 58 29 45 52 37 62 24 [2081] 41 39 49 74 33 31 32 26 55 12 6 69 51 54 10 0 [2097] 15 32 70 27 39 55 73 40 46 11 1 27 36 69 33 11 [2113] 74 69 45 34 70 51 62 52 37 22 51 3 56 79 38 45 [2129] 1 11 75 26 31 1 33 69 69 45 16 23 61 67 60 45 [2145] 49 52 42 76 16 68 56 31 5 23 59 41 77 40 4 36 [2161] 22 11 77 75 23 66 30 66 67 56 39 3 34 51 55 2 [2177] 36 21 2 0 73 55 52 70 47 40 68 30 68 48 28 26 [2193] 59 59 25 67 60 38 15 35 63 2 38 12 57 35 61 67 [2209] 62 30 55 66 8 18 41 63 5 26 52 25 67 46 2 17 [2225] 34 69 43 78 39 78 3 21 72 29 65 62 2 27 61 15 [2241] 23 22 25 29 30 78 60 49 63 6 31 18 39 73 12 17 [2257] 77 21 21 72 11 50 11 45 15 78 22 57 53 2 2 37 [2273] 32 41 74 70 44 34 12 78 34 13 46 3 5 55 43 62 [2289] 52 13 32 40 65 57 76 78 1 35 17 1 27 43 52 15 [2305] 54 67 46 42 20 30 14 12 58 42 14 76 64 35 25 51 [2321] 52 27 36 60 79 36 14 10 45 11 43 44 69 17 8 40 [2337] 73 4 37 1 17 75 0 41 58 74 42 4 53 39 6 18 [2353] 78 46 11 46 1 24 11 71 23 2 29 57 78 74 3 70 [2369] 22 58 18 36 54 61 49 76 42 67 53 23 28 16 25 78 [2385] 71 39 44 43 57 13 35 9 52 51 54 21 23 33 65 39 [2401] 21 31 15 58 26 79 58 57 48 57 9 11 19 38 9 58 [2417] 46 18 53 2 61 76 34 27 56 5 48 63 7 20 38 0 [2433] 28 5 3 59 43 46 68 60 64 35 1 77 33 76 37 42 [2449] 23 63 30 44 7 10 4 59 74 15 40 75 69 78 43 31 [2465] 30 72 37 44 69 9 37 77 61 54 43 1 29 5 43 30 [2481] 0 65 79 1 9 16 66 56 33 38 73 64 46 53 48 20 [2497] 22 79 23 5 44 12 7 49 46 78 28 10 78 3 13 79 [2513] 55 62 12 14 29 64 48 43 61 50 42 36 72 58 50 74 [2529] 67 29 78 12 2 16 9 37 74 69 56 15 54 12 51 14 [2545] 39 63 7 26 46 59 49 40 25 75 14 70 36 48 77 49 [2561] 33 53 79 15 14 35 24 7 71 17 60 40 19 13 19 65 [2577] 22 5 38 73 79 3 7 10 57 39 36 41 3 58 25 22 [2593] 51 39 19 17 73 75 2 11 54 57 76 61 56 5 71 72 [2609] 34 36 57 76 28 57 49 64 68 78 23 17 27 38 75 64 [2625] 60 2 13 28 29 73 19 18 13 6 42 25 43 40 6 2 [2641] 23 41 26 21 45 57 72 17 67 62 40 41 42 46 2 43 [2657] 66 63 46 54 73 58 43 20 6 47 26 70 28 19 29 10 [2673] 24 26 6 51 63 11 34 24 79 31 36 5 60 63 20 74 [2689] 18 20 35 42 41 63 32 61 3 25 7 40 14 4 16 11 [2705] 10 12 51 57 57 68 19 25 71 8 60 34 24 63 79 17 [2721] 33 18 16 53 3 37 5 70 10 15 31 46 45 9 38 78 [2737] 38 79 38 28 10 26 69 55 69 25 39 41 76 69 28 54 [2753] 31 71 59 79 9 43 51 63 57 64 43 8 50 23 4 69 [2769] 14 50 41 13 5 43 66 41 18 78 69 69 0 43 50 64 [2785] 17 56 44 12 40 60 68 67 49 73 53 39 64 3 36 3 [2801] 14 1 67 22 27 50 69 67 21 34 12 27 66 47 68 20 [2817] 67 11 25 43 33 28 30 33 40 56 6 79 22 12 4 27 [2833] 62 41 2 28 75 19 9 5 5 5 0 78 16 35 62 12 [2849] 41 77 76 34 14 71 24 5 66 49 41 16 75 55 20 50 [2865] 33 73 28 43 53 75 15 50 27 39 45 63 22 50 70 5 [2881] 26 71 56 67 21 16 31 18 9 18 61 3 61 53 36 55 [2897] 18 33 20 7 65 15 0 55 76 58 26 12 49 76 48 41 [2913] 47 69 44 67 56 74 64 56 61 57 39 39 58 60 57 33 [2929] 79 51 5 2 8 30 22 38 40 76 49 37 10 25 78 73 [2945] 9 36 38 7 72 27 58 44 29 73 27 58 53 60 73 61 [2961] 30 50 62 34 10 17 9 55 64 64 76 40 48 41 76 25 [2977] 39 6 56 56 6 33 39 43 65 74 70 73 4 17 14 76 [2993] 50 7 4 3 65 10 6 12 0 14 45 63 55 39 70 59 [3009] 12 22 69 44 30 54 32 75 31 33 33 25 27 22 4 21 [3025] 1 19 0 40 4 17 38 75 28 13 29 59 10 5 2 16 [3041] 23 22 8 57 14 78 9 39 68 40 51 14 32 16 48 72 [3057] 50 77 11 42 15 42 5 51 16 26 56 48 48 62 42 62 [3073] 3 62 42 79 16 56 64 2 26 29 26 39 61 71 17 36 [3089] 9 32 1 51 75 78 21 48 14 76 58 55 75 67 45 41 [3105] 1 14 76 39 60 45 30 73 50 33 78 73 64 46 33 7 [3121] 47 37 30 75 41 49 42 28 18 3 24 31 8 3 17 55 [3137] 20 1 77 3 6 26 75 16 22 32 28 51 27 17 18 67 [3153] 28 77 67 66 78 41 19 71 6 21 72 52 37 9 47 70 [3169] 2 28 60 7 29 40 78 55 41 2 24 11 11 54 43 62 [3185] 22 48 8 52 0 0 66 61 59 59 34 41 32 4 4 75 [3201] 78 30 54 61 27 2 25 62 49 60 5 72 4 77 67 58 [3217] 28 2 62 28 11 74 4 3 47 34 3 48 64 39 71 31 [3233] 79 24 75 4 50 5 60 21 35 27 10 46 24 59 19 57 [3249] 48 75 77 3 73 41 79 30 37 55 73 73 45 27 10 65 [3265] 31 53 63 16 36 15 35 71 0 5 7 63 22 8 46 45 [3281] 33 26 63 25 26 78 49 25 19 75 39 66 40 33 20 28 [3297] 21 38 76 24 75 65 11 34 63 24 58 25 70 47 57 33 [3313] 25 75 25 23 26 62 20 68 51 62 76 28 2 8 72 38 [3329] 62 32 29 10 57 9 19 34 38 39 26 21 13 28 46 45 [3345] 78 79 36 13 77 17 13 47 45 0 37 12 34 42 27 46 [3361] 74 64 44 16 26 60 23 32 8 68 5 50 29 27 52 53 [3377] 5 33 72 76 48 49 0 43 79 23 65 64 72 40 13 18 [3393] 50 40 30 59 41 68 72 38 4 17 33 43 6 72 5 1 [3409] 58 32 59 30 59 47 9 27 50 58 35 22 31 19 37 9 [3425] 45 29 39 51 33 23 12 36 1 60 39 10 17 59 0 25 [3441] 54 10 19 75 2 29 34 52 50 29 51 58 56 48 44 15 [3457] 73 20 45 43 41 5 53 34 19 47 37 47 76 15 34 71 [3473] 64 19 4 50 30 21 55 55 41 74 15 54 33 68 4 74 [3489] 51 0 62 14 3 63 50 42 49 66 22 57 12 8 5 20 [3505] 25 78 32 25 28 58 18 7 73 6 62 58 79 23 68 54 [3521] 35 48 27 23 50 1 0 52 32 55 17 54 43 41 35 64 [3537] 47 40 65 30 18 0 29 54 65 20 27 7 68 65 0 58 [3553] 24 44 75 23 71 7 21 71 10 21 56 66 66 55 66 51 [3569] 52 47 8 24 50 56 68 12 2 1 13 32 30 61 64 5 [3585] 41 3 35 32 23 20 70 51 4 9 62 15 74 8 55 65 [3601] 39 12 54 42 1 16 42 22 66 22 48 3 38 4 23 22 [3617] 76 15 33 27 30 75 12 71 67 67 27 27 9 28 35 70 [3633] 37 76 27 18 54 63 74 51 1 66 77 50 66 61 75 52 [3649] 70 46 63 20 46 72 76 29 75 72 68 21 56 19 28 21 [3665] 36 10 13 9 50 47 21 47 78 50 24 39 7 11 41 60 [3681] 7 49 21 65 16 11 17 13 64 72 74 12 45 74 47 27 [3697] 24 66 3 40 20 26 1 5 45 15 34 20 17 21 40 52 [3713] 71 20 74 13 4 7 14 78 74 42 24 37 8 48 33 24 [3729] 41 51 61 56 76 0 49 10 36 21 65 26 16 76 69 59 [3745] 21 1 45 19 6 69 32 70 40 78 61 37 46 60 15 42 [3761] 21 10 42 32 56 17 74 2 28 1 21 1 38 64 27 78 [3777] 52 31 59 15 67 74 31 62 65 34 24 3 24 42 37 34 [3793] 57 41 2 56 70 34 16 71 68 53 48 32 0 24 33 13 [3809] 35 11 56 24 37 40 31 66 43 47 45 36 19 37 31 67 [3825] 46 5 46 56 46 58 33 11 65 18 69 4 76 7 71 36 [3841] 54 71 14 17 7 77 36 2 23 55 79 22 68 65 13 61 [3857] 20 61 68 61 33 42 8 26 15 53 11 36 5 29 17 49 [3873] 42 27 17 45 39 44 43 36 58 72 53 2 18 10 11 54 [3889] 50 38 34 19 58 53 78 27 68 73 35 1 65 12 24 44 [3905] 24 13 17 30 5 15 50 64 37 50 64 33 10 11 30 45 [3921] 35 38 4 10 35 78 63 25 21 76 26 27 56 3 53 65 [3937] 68 73 54 55 35 36 75 11 46 66 19 4 6 61 64 25 [3953] 32 30 43 70 6 37 5 59 37 5 73 77 23 73 66 25 [3969] 26 19 18 58 0 9 53 37 10 57 61 44 31 11 47 36 [3985] 41 6 13 11 57 28 6 49 10 72 59 8 64 74 19 14 [4001] 65 19 52 45 61 53 43 47 74 63 42 44 55 8 31 38 [4017] 71 45 29 43 34 56 31 59 9 10 57 53 71 62 79 63 [4033] 10 58 61 26 53 45 17 17 22 44 14 67 74 55 18 18 [4049] 3 42 60 51 23 27 37 77 15 37 69 8 34 14 48 63 [4065] 11 48 22 11 46 64 66 52 52 11 0 63 17 44 22 68 [4081] 55 25 68 15 17 55 16 60 20 23 3 24 26 10 20 16 [4097] 60 72 20 22 31 63 53 37 37 62 16 8 16 69 30 63 [4113] 1 46 71 53 10 71 18 28 28 31 29 11 15 62 70 76 [4129] 5 34 5 36 55 73 48 30 75 51 5 49 3 10 5 21 [4145] 51 6 74 4 75 45 53 6 40 48 59 33 65 50 22 15 [4161] 11 44 35 70 70 15 66 24 46 13 70 21 37 31 59 67 [4177] 33 0 75 52 61 23 51 43 9 55 66 17 63 74 19 22 [4193] 27 11 9 52 18 13 53 26 26 51 56 39 9 41 50 30 [4209] 67 48 31 16 49 11 11 2 28 62 53 30 49 79 32 31 [4225] 54 19 51 41 14 9 4 29 71 11 12 34 69 4 12 31 [4241] 18 52 73 13 23 47 2 76 34 32 23 68 22 41 36 52 [4257] 62 37 9 49 34 33 8 70 18 67 25 43 26 3 22 39 [4273] 61 47 61 38 69 9 17 61 36 74 39 21 70 48 69 58 [4289] 54 30 48 67 2 5 34 43 30 29 9 58 32 10 11 9 [4305] 52 47 17 45 27 32 53 16 40 35 54 72 1 25 51 6 [4321] 32 66 13 71 36 36 47 31 66 20 40 28 27 68 18 75 [4337] 15 28 63 46 37 69 54 29 13 75 22 79 29 69 36 50 [4353] 77 32 25 32 57 57 37 62 6 76 47 72 5 66 45 70 [4369] 48 24 78 56 32 73 70 49 20 24 13 35 19 38 39 56 [4385] 70 33 67 38 73 63 69 4 62 7 4 9 32 76 30 11 [4401] 7 75 23 79 7 56 16 64 47 59 40 60 65 0 17 63 [4417] 13 69 61 44 42 50 15 73 22 48 50 40 13 70 74 31 [4433] 48 44 39 46 79 78 27 26 28 8 28 5 39 10 79 49 [4449] 66 34 74 6 24 30 41 24 70 61 27 34 65 45 58 57 [4465] 35 47 57 35 29 55 1 11 24 71 33 79 45 29 62 55 [4481] 78 38 27 20 63 19 32 33 22 52 17 74 6 46 44 55 [4497] 72 58 23 40 38 60 0 65 14 18 68 21 0 4 19 69 [4513] 57 67 46 6 31 2 10 29 6 70 24 67 35 0 56 66 [4529] 8 41 24 63 74 74 51 7 51 31 66 58 28 75 23 60 [4545] 75 49 7 8 68 8 70 37 72 30 53 15 48 30 79 53 [4561] 20 8 1 26 60 44 30 0 50 40 16 35 39 57 77 41 [4577] 58 37 66 34 50 27 76 8 65 47 7 9 14 6 48 13 [4593] 8 6 29 6 72 26 60 1 38 16 74 8 50 7 33 17 [4609] 72 15 32 66 45 72 50 63 12 17 47 46 14 35 77 4 [4625] 76 4 14 8 68 23 65 25 45 3 18 13 26 0 69 22 [4641] 72 31 42 35 40 24 60 38 77 3 59 60 4 54 71 64 [4657] 76 62 21 38 78 26 6 59 77 10 25 74 31 67 77 42 [4673] 50 10 17 54 79 20 30 63 46 38 5 28 53 32 30 1 [4689] 54 76 45 37 36 32 13 13 58 74 46 60 57 9 40 60 [4705] 50 26 0 58 14 31 8 69 5 34 74 78 35 44 71 19 [4721] 74 27 17 71 49 34 73 68 49 16 69 31 51 57 45 69 [4737] 2 52 76 71 5 52 13 77 69 22 42 79 42 27 36 16 [4753] 12 70 25 33 66 17 75 67 67 66 32 3 79 49 70 19 [4769] 62 5 2 60 10 56 78 7 25 56 30 66 2 1 45 32 [4785] 36 26 63 58 39 28 15 73 10 64 78 64 17 60 16 67
Visualization
Bar plot
Representing the sample with a single value
\[\begin{aligned} \text{mean}(\mathbf x)&=\frac{1}{N}\sum_i x_i\\ &=\bar{\mathbf x}\end{aligned}\]
mean(x) is the average of x
\(\bar{\mathbf x}\) is the value that results in the smallest squared error
mean(pop_LD)
[1] 4.5
mean(pop_MD)
[1] 14.5
mean(pop_HD)
[1] 39.5
Variance: Quality of representation
\[\text{var}(\mathbf x)=\frac{1}{N}\sum_i (x_i-\bar{\mathbf x})^2\]
Variance is the mean squared error of the average
We explained this on the last semester
var(pop_LD)
[1] 8.25
var(pop_MD)
[1] 74.9
var(pop_HD)
[1] 533
standard deviation
\[\begin{aligned} \text{sd}(\mathbf x)&=\sqrt{\text{var}(\mathbf x)}\\ &=\sqrt{\frac{1}{N}\sum_i (x_i-\bar{\mathbf x})^2}\end{aligned}\]
sd(pop_LD)
[1] 2.87
sd(pop_MD)
[1] 8.66
sd(pop_HD)
[1] 23.1
Standard Deviation is the “width” of population
We care about sd(x) because it tells us how close is the mean to most of the population
Russian mathematician Chebyshev It can be proved that always \[\Pr(\vert x_i-\bar{\mathbf x}\vert\geq k\cdot\text{sd}(\mathbf x))\leq 1/k^2\]
In other words, the probability that “the distance between the mean \(\bar{\mathbf x}\) and any element \(x_i\) is bigger than \(k\cdot\text{sd}(\mathbf x)\)” is less than \((1/k^2)\)
This is Chebyshev’s inequality
It is always valid, for any probability distribution
(Later we will see better rules valid only sometimes)
It can also be written as \[\Pr(\vert x_i-\bar{\mathbf x}\vert\leq k\cdot\text{sd}(\mathbf x))\geq 1-1/k^2\]
The probability that “the distance between the mean \(\bar{\mathbf x}\) and any element \(x_i\) is less than \(k\cdot\text{sd}(\mathbf x)\)” is greater than \(1-1/k^2\)
Some examples of Chebyshev’s inequality
Another way to understand the meaning of this theorem is \[\Pr(\bar{\mathbf x} -k\cdot\text{sd}(\mathbf x)\leq x_i \leq \bar{\mathbf x} +k\cdot\text{sd}(\mathbf x))\geq 1-1/k^2\] Replacing \(k\) for some values, we get \[\begin{aligned} \Pr(\bar{\mathbf x} -1\cdot\text{sd}(\mathbf x)\leq x_i \leq \bar{\mathbf x} +2\cdot\text{sd}(\mathbf x))&\geq 1-1/1^2=0\\ \Pr(\bar{\mathbf x} -2\cdot\text{sd}(\mathbf x)\leq x_i \leq \bar{\mathbf x} +2\cdot\text{sd}(\mathbf x))&\geq 1-1/2^2=0.75\\ \Pr(\bar{\mathbf x} -3\cdot\text{sd}(\mathbf x)\leq x_i \leq \bar{\mathbf x} +3\cdot\text{sd}(\mathbf x))&\geq 1-1/3^2=0.889 \end{aligned}\]
Explanation from stats.libretexts.org
For any numerical data set
- at least 3/4 of the data lie within two standard deviations of the mean, that is, in the interval with endpoints \(\bar{\mathbf x}±2\cdot\text{sd}(\mathbf x)\)
- at least 8/9 of the data lie within three standard deviations of the mean, that is, in the interval with endpoints \(\bar{\mathbf x}±3\cdot\text{sd}(\mathbf x)\)
- at least \(1-1/k^2\) of the data lie within \(k\) standard deviations of the mean, that is, in the interval with endpoints \(\bar{\mathbf x}±k\cdot\text{sd}(\mathbf x),\) where \(k\) is any positive whole number greater than 1
Example: the case of pop_HD
These values should be less than 1, 0.25 and 0.11
mean(abs(pop_HD-mean(pop_HD))> 1*sd(pop_HD))
[1] 0.425
mean(abs(pop_HD-mean(pop_HD))> 2*sd(pop_HD))
[1] 0
mean(abs(pop_HD-mean(pop_HD))> 3*sd(pop_HD))
[1] 0
Sampling
Simulating cell counting
one_sample <- function(m, population) {
return(sample(population, size=m))
}
one_sample(30, pop_HD)
[1] 32 40 62 43 71 47 44 17 41 27 65 11 69 23 46 19 7 [18] 30 29 34 17 58 70 75 53 15 68 57 29 35
Sample mean is a random variable
Bad news!
The sample average changes every time
Moreover, it is often different from the population average
Sample average v/s size
Sample average v/s size
Average of smaller samples are more extreme
Average of smaller samples are more extreme
This explains why rural areas have the highest and lowest cancer rates
It is because the groups are smaller, so averages are taken from smaller groups
We saw the same on the GC content
Good news
When the sample size is big,
the sample average is closer to
the population average
Variation depends on sample size
Log-log plot (for high density population)
plot(log(sd_sample_mean)~log(size)) model_HD <- lm(log(sd_sample_mean)~log(size)) lines(predict(model_HD)~log(size))
Linear model
coef(model_HD)
(Intercept) log(size)
3.242 -0.528
\[\log(\text{sd_sample_mean}) = 3.242 + -0.528\cdot\log(\text{size})\] \[\text{sd_sample_mean} = \exp(3.242) \cdot\text{size}^{-0.528} =25.587\cdot\text{size}^{-0.528}\]
Models for all populations
\[\text{sd_sample_mean} = A\cdot \text{size}^B\]
| A | B | std dev population | |
|---|---|---|---|
| pop_LD | 3.282 | -0.5306 | 2.873 |
| pop_MD | 9.092 | -0.5126 | 8.656 |
| pop_HD | 25.59 | -0.528 | 23.09 |
Coefficient \(A\) is the standard deviation of the population
Coefficient \(B\) is -0.5
What does this mean
If we know the population standard deviation, we can predict the sample standard deviation
\[\text{sd(sample mean)}=\frac{\text{sd(population)}}{\sqrt{\text{sample size}}}\]
Law of Large Numbers
Using Chebyshev formula, we know that, with high probability \[\vert \text{mean(sample)} -\text{mean(population)}\vert < k\cdot\frac{\text{sd(population)}}{\sqrt{\text{sample size}}}\]
Therefore the population average is inside the interval \[\text{mean(sample)} \pm k\cdot\frac{\text{sd(population)}}{\sqrt{\text{sample size}}}\] (probably)
How to know population standard deviation?
Remember that we do not know neither the population mean nor the population variance
So we do not know the population standard deviation 😕
In most cases we can use the sample standard deviation
Visually
Central Limit Theorem
Francis Galton, his cousin and his machine
English explorer, Inventor, Anthropologist
(1822–1911)
Cousin of Charles Darwin
He studied medicine and mathematics at Cambridge University.
He invented the phrase “nature versus nurture”
In his will, he donated funds for a professorship in genetics to University College London.
Galton Machine
Simulated Galton Machine
Simulating the Galton Machine
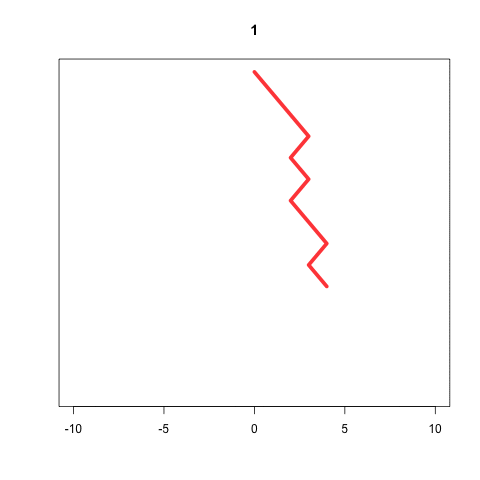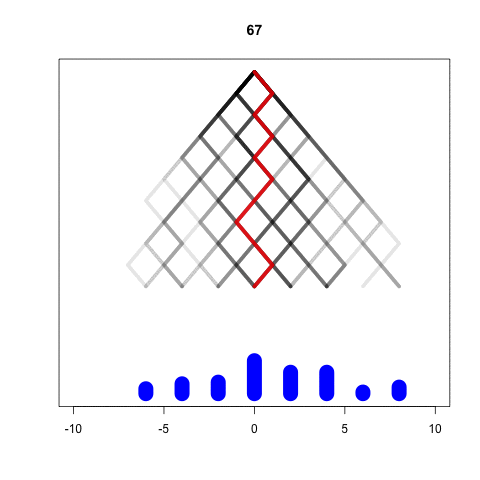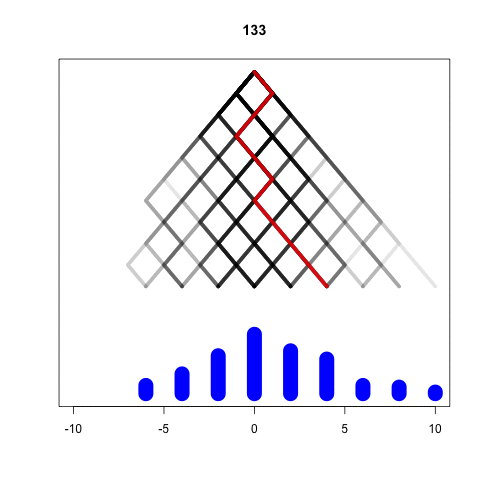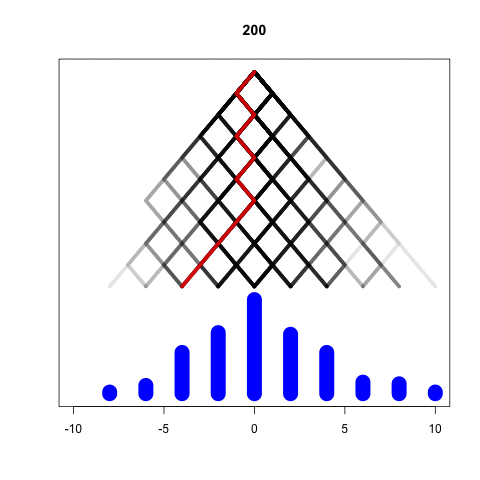
We will simulate each ball one by one
one_ball <- function(M) {
return(sum(sample(c(-1,1), size=M, replace=TRUE)))
}
Here M is the number of “left-right” choices made by the ball
Simulating the Galton Machine
Galton <- replicate(1000, one_ball(5)) barplot(table(Galton))
Bigger M, wider variance
Galton <- replicate(10000, one_ball(50)) barplot(table(Galton))
Bigger M gives wider results
Variances
Mean and Variance
It is easy to see that the population mean is 0 for any M
If we think, we can show that the variance is M
Standard deviation will be sqrt(M)
correcting variance M=5
Galton <- replicate(10000, one_ball(5))/sqrt(5) barplot(table(Galton))
correcting variance M=50
Galton <- replicate(10000, one_ball(50))/sqrt(50) barplot(table(Galton))
correcting variance M=500
Galton <- replicate(100000, one_ball(500))/sqrt(500) barplot(table(Galton))
correcting variance M=5000
Galton <- replicate(100000, one_ball(5000))/sqrt(5000) barplot(table(Galton))
When M is big, we get Normal distribution
The Normal distribution
This “bell shaped” curve is found in many experiments, specially when they involve the sum of many small contributions
- Measurement errors
- Height of a population
- Scores on University Admission exams
It is called Gaussian distribution, or also Normal distribution
Simulating the Normal distribution
Instead of simulating the Galton machine several times, we can simulate the Normal distribution using the R function
rnorm(n, mean = 0, sd = 1)
The parameter n is mandatory. It is the sample size
You can also change the mean and the standard deviation of the simulation
Exercise
In Class 8 (and Homework 8) we predicted the final outcome of the water formation for each value of r1_rate, and fixing the other values
rates_of_r1 <- 10^seq(from=-3, to=-1, length=50) r2_rate=0.01, H_ini=2, O_ini=1, W_ini=0
Now we are not so sure about how much hydrogen we had at the beginning. Instead of H_ini=2 fixed, we will simulate taking values from
H_values <- rnorm(n=6, mean=2, sd=0.05)
You should get a plot like this
