April 19, 2019

A comment about the exam

Questions are based on published papers

There is a new book from the same author

It is about epidemiology

The same models are used for real diseases

  • Ebola
  • Zika
  • Epidemics
  • Parasites
    • in Plants
    • in Humans

Question 3.1

N <- 28*24
movie <- horror_movie(N, human_ini=2, dead_ini=1,
    zombie_ini=0, attack_rate = 5e-3, kill_rate=1e-3,
    voodoo_rate=1e-2)

Given the initial conditions and the rates, we can predict what will happen

Question 3.2

Please make a vector called rate_of_kill with one hundred values between 1e-3 and 1e-1.

Then create two empty vectors called final_human and final_zombie with the same length of rate_of_kill.

For each value in rate_of_kill simulate the horror_movie system with the same initial values, attack rate and voodoo rate, and changing kill_rate for the corresponding value in rate_of_kill. Store the value of human at the last hour of each simulation in the vector final_human. Do the same with the last value of zombie, storing it into final_zombie.

Answer to Question 3.2

rate_of_kill <- seq(1e-3, 1e-1, length.out = 100)
final_human <- rep(NA, length(rate_of_kill))
final_zombie <- rep(NA, length(rate_of_kill))
for(i in 1:length(rate_of_kill)) {
    movie <- horror_movie(N, human_ini=2, dead_ini=1,
        zombie_ini=0, attack_rate = 5e-3, 
        kill_rate=rate_of_kill[i], voodoo_rate=1e-2)
    final_human[i] <- movie$human[N]
    final_zombie[i] <- movie$zombie[N]
}

Result

rate_of_kill <- seq(1e-3, 1e-1, length.out = 100)
human_ini=2, dead_ini=1, zombie_ini=0,
attack_rate = 5e-3, voodoo_rate=1e-2

We can predict changes in output when there are changes in input

Consider the water formation system

We can predict how much water we will have

mix <- water_formation(N=200, r1_rate=0.01, r2_rate=0.01,
     H_ini=2, O_ini=1, W_ini=0)
plot(Water~Step, data=mix, ylim=c(0, 1), type="l")

Amount of water depends on r1_rate

rates_of_r1 <- 10^seq(from=-3, to=-1, length=5)
r2_rate=0.01, H_ini=2, O_ini=1, W_ini=0

We can predict final outcome for each rate

rates_of_r1 <- 10^seq(from=-3, to=-1, length=5)
r2_rate=0.01, H_ini=2, O_ini=1, W_ini=0

Same with more r1_rate values

rates_of_r1 <- seq(from=0.001, to=0.1, length=50)
r2_rate=0.01, H_ini=2, O_ini=1, W_ini=0

This is the same pattern as Question 3.2

final_Water <- rep(NA, length(rates_of_r1))
for(i in 1:length(rates_of_r1)) {
    mix <- water_formation(N=100, r1_rate=rates_of_r1[i],
                r2_rate=0.01, H_ini=2, O_ini=1, W_ini=0)
    final_Water[i] <- mix$Water[100]
}
plot(rates_of_r1, final_Water)

How can we know the reaction rate?

what was the reaction rate?

We can measure how much water we got. If at the end we have 0.5 mol of water, then … … with the curve we can find what was the reaction rate

Why we do Science

Nature exists outside us

We observe nature

We want to understand Nature

We see that Nature has rules

Everything happens with a cause

Science is the process of discovering the rules of Nature

The Scientific Method

Systems are Models/Explanations

The systems we have seen are used to explain what happens

They are simplifications of reality

We discard details that we think are irrelevant

If the system makes bad prediction, the system is wrong

Systems are in a state

  1. The particular condition that someone or something is in at a specific time
    • water in a liquid state.
  2. The amounts of all items (circles) in a system.
    • water[i]
    • hydrogen[i]

The state of the system changes with time

In any fixed time, the state has fixed values

  • one value for each item
  • Examples:
    • water[i], hydrogen[i]
    • Number of cats and mice
    • Number of primers and DNA molecules
    • Number of humans and zombies

The state today depends only on the past states

The “arrows” of the system do not change with time

The new state depends only on the past states, nothing else

If we know the initial state and rate constant, we can calculate everything

We do experiments to discover the current state of the system

“An intelligence knowing all the forces acting in nature at a given instant, as well as the momentary positions of all things in the universe, would be able to comprehend in one single formula the motions of the largest bodies as well as the lightest atoms in the world; to it nothing would be uncertain, the future as well as the past would be present to its eyes.”

Pierre-Simon Laplace, French mathematician and astronomer (1749 – 1827)

What Laplace said

  • “all the forces acting in nature at a given instant, as well as the momentary positions of all things in the universe”

    If we know the current state …

  • “would be able to comprehend in one single formula the motions of the largest bodies as well as the lightest atoms in the world

    And we know the system…

If we know the system and the current state…

  • “nothing would be uncertain, the future as well as the past would be present”

    Then we can know exactly what is in the future

These are deterministic systems

All the future is determined
by the initial state
and the system rules

Can we really predict the future?

Sometimes we can predict

Sometimes models are too simple and they miss important parts

If the system is realistic, we can predict

We need to measure initial values and rates

But all measurements have a margin of error

What if we don’t know the exact value?

In real life we cannot measure exact values

We can only measure within a margin of error

For example, when we measure 2.0 mol of Hydrogen, it may be 1.95 or 2.05 or any value in between

Inaccurate measurement of H_ini

Small initial errors give small final errors

Effect of error on r1_rate evaluation

Small changes in initial state produces small changes in final state

Even if we make errors, their effect is not very important

Another system: Quadratic map

  • A population that reproduces and dies
  • Death happens in pairs (two incoming arrows)

Another system: Quadratic map

To study this system, we will assume that death rate and birth rate depend on a single value A

  • Death rate is A/2
  • Birth rate is A-1
  • If we know A, we know birth and dead rate

Formulas are easy to find

d_x[i] <- (A-1) * x[i-1] - 2 * A/2 * x[i-1]*x[i-1]
x[i]   <- x[i-1] + d_x[i]

in other words

x[i] <- x[i-1] + (A-1) * x[i-1] - 2 * A/2 * x[i-1]*x[i-1]

so finally

x[i] <- A * x[i-1] * (1 - x[i-1])

and the program is also easy to write

quad_map <- function(N, A, x_ini) {
  x <- rep(NA, N)
  x[1] <- x_ini
  for(i in 2:N) {
    x[i] <- A * x[i-1] * (1 - x[i-1])
  }
  return(x)
}

We simulate for different initial conditions

x_ini <- c(0.4, 0.45, 0.5, 0.55, 0.6)
ans <- data.frame(V1=quad_map(N=100, x_ini=x_ini[1], A=2))
plot(ans$V1, ylim=c(0,1), ylab="x", type="b")
for(i in 2:length(x_ini)) {
    ans[[i]] <- quad_map(N=100, x_ini=x_ini[i], A=2)
    points(ans[[i]], pch=i, type="b")
}

The final state is always the same

This is called attractor

Behavior depends on A. Here A=3

Now there are two final states.
This is a periodic attractor

Behavior depends on A. Here A=3.5

Now we have four final states.
Also a periodic attractor

Behavior depends on A. Here A=3.8

We do not see a pattern here

Behavior depends on A. Here A=3.95

Similar initial states, very different results

Small changes in x_ini, big changes in result

Initial values:

x_ini
[1] 0.40 0.45 0.50 0.55 0.60

Final values:

ans[100,]
            V1        V2        V3        V4        V5
100 0.07712169 0.7034133 0.8541633 0.7034133 0.4900459

There is a Pattern

Here we see the final 500 states for different values of A 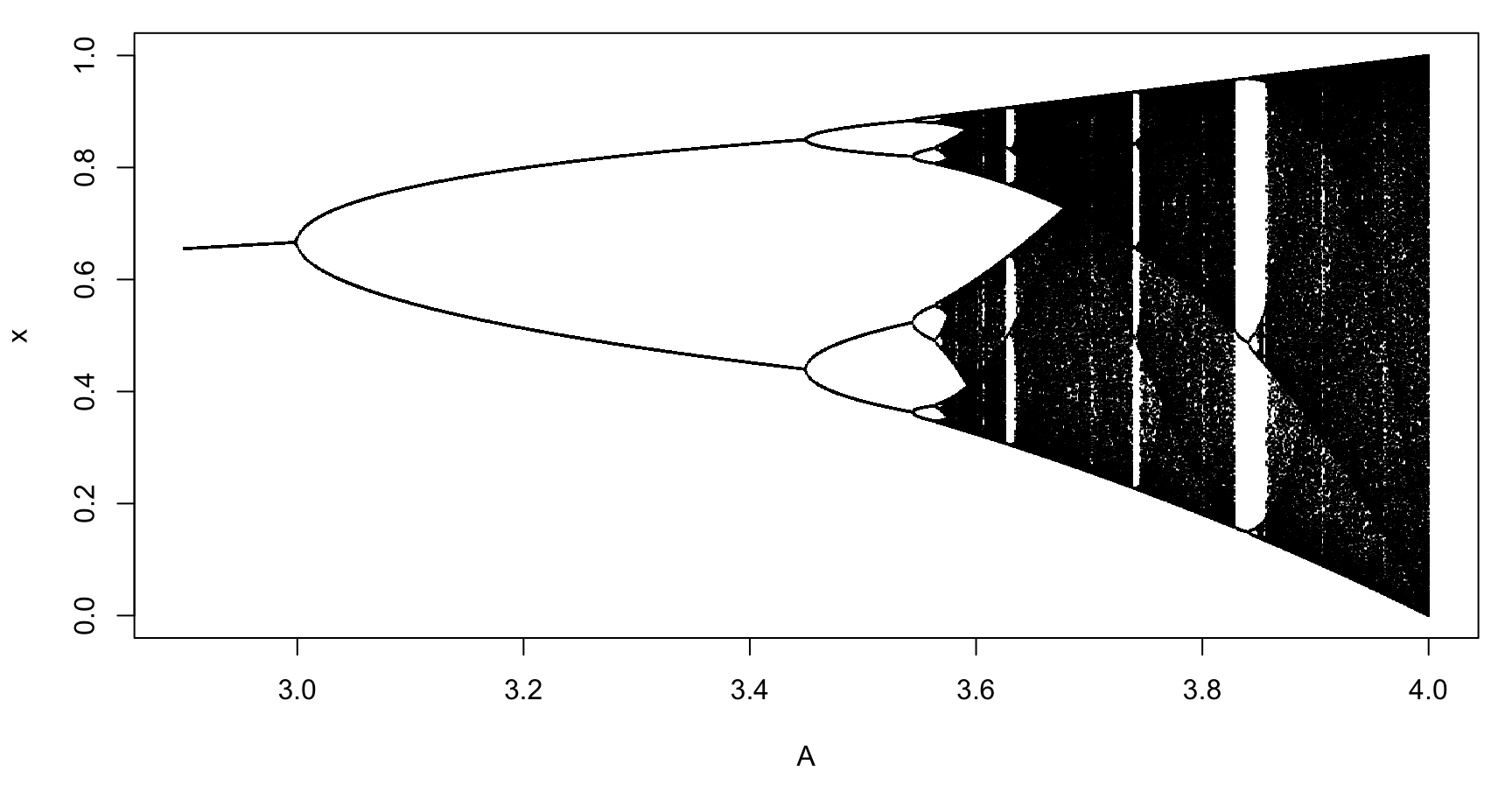Homework: do this plot. More details later

We cannot predict

well, not always

This is called “Butterfly Effect”

The fly of a butterfly in Istanbul can produce an hurricane in Mexico

Small changes have big consequences

But we can still say something

We cannot make exact predictions

But we can still say what is normal

What is the most probable behavior

We can identify patterns using the tools of …. (sound of drums)

Probabilities

Not about games and bets

People think that probabilities are about games

Instead they are really tools for thinking

Thinking about decisions when we have incomplete information

Thinking about the future

About the meaning of our experiment results

Do you need probabilities?

Do you travel?

  • Which is the safest way to travel?
  • Which is the fastest way to travel?
  • How much do you want to pay for safety?
  • How much do you want to pay for speed?

Do you buy insurance?

Sigorta

Travel insurance, Health insurance

  • how much do you pay for it?
  • How much you will get paid?
  • Is it worth it?

Why do you study?

  • You can work now and earn money today
  • What if you fail this course?
  • Why if you do not find a job?

Will you make experiments?

  • How will you understand the results?
  • Are the results just “random noise”?
  • What are your expected results
    • Allele frequency
    • Success rate of a treatment

All these questions are about probabilities

To understand the idea we will use games

  • Cards
  • Coins
  • Dice (one die, many dice)

maybe other toys that are easy to understand

These are just to have easy examples

What can happen: outcomes

Each device has a set of possible outcomes:

For example a die has the following outcomes

⚀ ⚁ ⚂ ⚃ ⚄ ⚅

Cards

🂡 🂢 🂣 🂤 🂥 🂦 🂧 🂨 🂩 🂪 🂫 🂭 🂮 🂱 🂲 🂳 🂴 🂵 🂶 🂷 🂸 🂹 🂺 🂻 🂽 🂾 🃁 🃂 🃃 🃄 🃅 🃆 🃇 🃈 🃉 🃊 🃋 🃍 🃎 🃑 🃒 🃓 🃔 🃕 🃖 🃗 🃘 🃙 🃚 🃛 🃝 🃞 🃟

Also Cards

♠︎♣︎♡♢

Four symbols can be used to represent DNA

A, C, G, T

Coins

Head, Tail also written as H, T

Doing the experiment is easy

just throw the dice

Simulating the experiment in R

We know how to represent outcomes

  • Coin: c("H","T")
  • Dice: 1:6
  • Cards/DNA: c("a","c","g","t")
  • Capital Letters: LETTERS
  • Small Letters: letters

Please take a sample()

Try this

sample(LETTERS)
 [1] "O" "S" "Z" "R" "C" "K" "X" "I" "J" "W" "E" "P" "H" "Y" "B" "A" "Q"
[18] "N" "D" "M" "V" "F" "G" "U" "L" "T"
sample(LETTERS)
 [1] "A" "X" "I" "M" "F" "G" "B" "J" "V" "D" "C" "R" "Y" "O" "U" "N" "H"
[18] "W" "Q" "L" "K" "Z" "P" "T" "E" "S"

sample() is shuffling

The output has the same elements of the input but in a different order

Each element appears only once

The order changes every time

Choosing the sample size

Try this

sample(LETTERS, size=10)
 [1] "R" "B" "U" "F" "W" "N" "L" "G" "Z" "O"

We get 10 letters. Some, but not all input elements

Each element appears only once

Sampling many elements

Try this

sample(c("H","T"), size=10)
Error in sample.int(length(x), size, replace, prob): cannot take a sample larger than the population when 'replace = FALSE'

We run out of elements

Sampling with replacement

Try this

sample(c("H","T"), size=10, replace=TRUE)
 [1] "H" "T" "T" "T" "T" "T" "H" "T" "T" "T"

Each element can appear several times

Shuffle, take one, replace it on the set

Most of times we will use sample() with replace=TRUE

Is there a pattern in the result?

table(sample(c("a","c","g","t"), size=40, replace=TRUE))
 a  c  g  t 
 8 16  6 10 
table(sample(c("a","c","g","t"), size=40, replace=TRUE))
 a  c  g  t 
 5  8 10 17 
table(sample(c("a","c","g","t"), size=40, replace=TRUE))
 a  c  g  t 
13 13  7  7

Each result is different

Is there a pattern in the result?

table(sample(c("a","c","g","t"), size=400, replace=TRUE))
  a   c   g   t 
 90 124  88  98 
table(sample(c("a","c","g","t"), size=400, replace=TRUE))
  a   c   g   t 
115  97  97  91 
table(sample(c("a","c","g","t"), size=400, replace=TRUE))
  a   c   g   t 
120 105  79  96

When size increases, the frequency of each letter also increases

Is there a pattern in the result?

table(sample(c("a","c","g","t"), size=4000, replace=TRUE))
   a    c    g    t 
1002  975 1015 1008 
table(sample(c("a","c","g","t"), size=4000, replace=TRUE))
   a    c    g    t 
 992  995 1025  988 
table(sample(c("a","c","g","t"), size=4000, replace=TRUE))
   a    c    g    t 
 988  998 1001 1013

When size increases, the frequencies change less

Is there a pattern in the result?

table(sample(c("a","c","g","t"), size=40000, replace=TRUE))
    a     c     g     t 
10098  9970  9950  9982 
table(sample(c("a","c","g","t"), size=40000, replace=TRUE))
    a     c     g     t 
 9948  9992 10088  9972 
table(sample(c("a","c","g","t"), size=40000, replace=TRUE))
    a     c     g     t 
 9980  9914 10157  9949

Each frequency is very close to 1/4 of size

Is there a pattern in the result?

table(sample(c("a","c","g","t"), size=400000, replace=TRUE))
     a      c      g      t 
100165  99999  99621 100215 
table(sample(c("a","c","g","t"), size=400000, replace=TRUE))
     a      c      g      t 
100172  99885  99776 100167 
table(sample(c("a","c","g","t"), size=400000, replace=TRUE))
     a      c      g      t 
100002 100216  99604 100178

If size increases a lot, the relative frequencies are 1/4 each

The sum of Relative Frequencies is 1

Absolute frequency is how many times we see each value
The sum of all absolute frequencies is the Total number of cases

Relative frequency is the proportion of each value in the total
The sum of all relative frequencies is always 1.

  • Relative frequency = Absolute frequency/Total number of cases

Relative Frequencies in our example

table(sample(c("a", "c", "g", "t"), size=1000000, replace=TRUE))/1000000
       a        c        g        t 
0.250345 0.249476 0.249657 0.250522

What is the final relative frequency?

What will be each relative frequency when size is BIG

In this case we can find it by thinking

  • There are 4 possible outcomes, and they are symmetrical
  • There is no reason to prefer one outcome to the other
  • Therefore all relative frequencies must be equal
  • Therefore each one must be 1/4

This ideal relative frequency is called Probability

Probabilities

Each device or random system may have some preferred outcomes

All outcomes are possible, but some can be probable

In general we do not know each probability

But we can estimate it using the relative frequency

That is what we will do in this course

Homework

Write the code to make the plots of this class