March 14, 2018
DNA has two strands
DNA has two strands
FASTA files show only one strand
We call it the forward strand
The other strand is not shown, but can be calculated
We call it the reverse strand
Calculating the reverse strand
According to Watson & Crick, the reverse strand is complementary
- Change
abytand vice-versa - Change
cbygand vice-versa
Moreover, the reverse strand is reversed
- 5’ becomes 3’ and vice-versa
- i.e. we have to read it backwards
opposite_strand <- function(dna) {
ans <- rep(NA, lenght(dna))
for(i in 1:lenght(ans)) {
j <- lenght(dna) - i + 1
if(dna[j]=='a') {
ans[i] <- 't'
} else if(dna[j]=='c') {
ans[i] <- 'g'
} else if(dna[j]=='g') {
ans[i] <- 'c'
} else if(dna[j]=='t') {
ans[i] <- 'a'
}
}
return(ans)
}
Another solution
Remember that we can give names to the elements of a vector
and we ca use the name as index
opposite_strand <- function(dna) {
ans <- rep(NA, lenght(dna))
compl <- c(a='t', c='g', g='c', t='a')
for(i in 1:lenght(ans)) {
j <- lenght(dna) - i + 1
ans[i] <- compl[ dna[j] ]
}
return(ans)
}
What happens if we use the reverse strand
Will GC content change?
Will GC skew change?
DNA statistics
Local DNA statistics
In the previous class we calculated GC content and GC skew for the complete genome
Now we want to calculate them in regions of the genome
This way we can see if there are differences in DNA composition
These differences can have biological importance
How to calculate values on regions
We will calculate the same formula on several DNA regions
Since it is the same pattern, we will prepare a function
What should be
- the output?
- the input(s)?
- the name?
Defining a GC skew function
Remember that an R function is defined like this
name <- function(input1, input2, ...) {
Calculate
return(output)
}
The inputs
The GC skew result should depend on:
- the genomic sequence
- the start of the region
- the length of the region
These are the parameters of the function. Do they have
- a name?
- a default value?
Note: avoid names that are already used for R functions
The output
Here we have two cases
For
gc_content()the output is a number with the value \[\frac{G+C}{A+T+G+C}\]For
gc_skew()the output is a number with the value \[\frac{G-C}{G+C}\]
In both cases the values in the formula are the number of nucleotides on the region
The steps from input to output
How do we transform the input parameters into the output value?
We can use any R function available, such as
seq(from, to, by, length.out)
Note: each input of seq() is optional
A possible solution
gc_content <- function(dna) {
freq <- table(dna)
ans <- (freq["g"]+freq["c"])/length(dna)
return(ans)
}
New Version:
gc_content <- function(dna, start=1, size=length(dna)) {
freq <- table(dna[seq(from=start, length.out=size)])
ans <- (freq["g"]+freq["c"])/size
return(ans)
}
Can you do the same for gc_skew()?
Applying the function to many values
We want to evaluate gc_content() and gc_skew() on different positions of the genome
We traverse the genome with non-overlapping windows of fixed size
position <- seq(from=1, to=length(dna), by=window_size)
How do we apply gc_skew() to each element of position?
One sample solution
position <- seq(from=1, to=length(dna), by=window_size)
for(i in 1:length(position)) {
skew[i] <- gc_skew(dna, position[i], window_size)
}
What is wrong here?
We cannot use [] if the vector does not exist
The first time we say skew[i] the vector skew does not exist
It has to be created before used
We can create it with just
skew <- NA
It is better if we declare the size
skew <- rep(NA, lenght(position))
Complete code to evaluate local GC skew
window_size <- 1E5
position <- seq(from=1, to=length(dna), by=window_size)
skew <- rep(NA, length(position))
for(i in 1:length(position)) {
skew[i] <- gc_skew(dna, position[i], window_size)
}
Result
plot(position, skew, type="l",
main=paste("window_size", window_size))
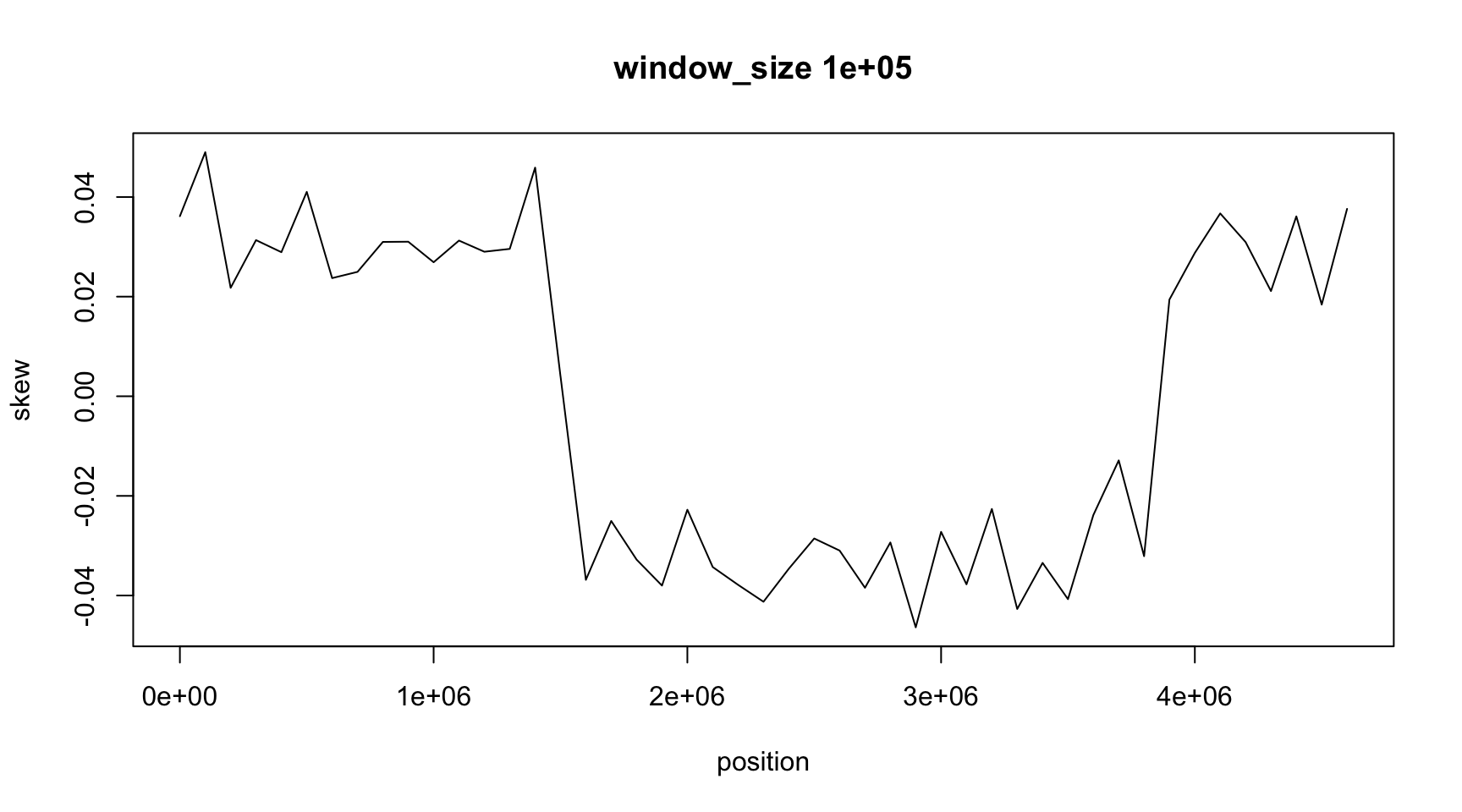
The result depends on window_size
Can you calculate the local G skew for different window sizes?
Are they equal or different?
Can you calculate local GC content?
Is local GC content different in different parts of DNA?
Result

Result

Result

Result

Finding the origin
As we discussed on the last class,
- the GC skew is positive in one part of chromosome
- and negative on the other, on average
- it changes sign in two places
The reason for this asymmetry is the DNA replication process
The origin of replication is in one of the sign changing places
How can we find the change of sign
We want to write a program so we can find Ori on many different genomes
We can answer questions like:
- Are both replichores of the same size?
- If they are different, what is the biological reason?
- Is there some insertion?
- What are the extra genes? What do they do?
Finding the change of sign is not so easy
The values can change a lot between a window and the next one
Can you plot the GC-skew of each window versus the next window?
each point is (skew[i],skew[i+1])
There is an easier way to find Ori
skew data is noisy. A lot of small random changes
Instead of looking directly at skew, we can look at cumulative skew
\[\text{cum_skew}[i]=\sum_{j=1}^i \text{skew}[j]\]
Now, instead of the change of sign, we look for the minimum and maximum (Why?)
How can we calculate cum_skew?
Cumulative sum
It is easy to see that
\[\text{cum_skew}[i]=\text{cum_skew}[i-1] + \text{skew}[i]\]
So we can write something like this:
cum_skew[1] <- skew[1]
for(i in 2:length(skew)) {
cum_skew[i] <- cum_skew[i-1] + skew[i]
}
Can you write this as a function?
Max & Min show the change of sign

Locating origin depends on window size
max(cum_skew)
[1] 4.9877
which.max(cum_skew)
[1] 155
position[which.max(cum_skew)]
[1] 1540001
Ori is located between position[which.max(cum_skew)] and position[which.max(cum_skew)] + window_size
How small can window_size be?
We can make the window very small
How would be skew and cum_skew if window_size=1