Last class we replaced distance by score
Distance has to be small, score has to be large
We replaced min by max
For global alignment it is the same
But for semi-global alignment it is different
November 20, 2018
Last class we replaced distance by score
Distance has to be small, score has to be large
We replaced min by max
For global alignment it is the same
But for semi-global alignment it is different
We have seen how to calculate the optimal score
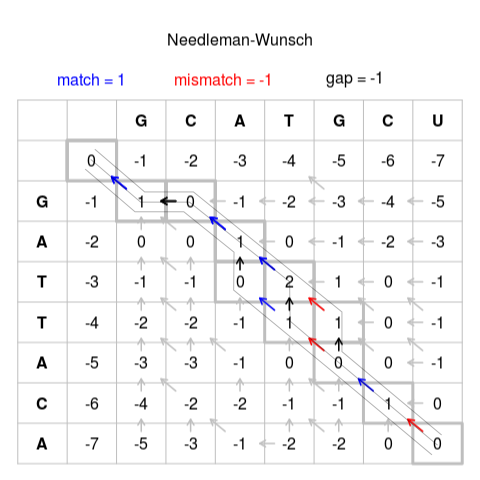
Needleman-Wunsh method tells us how to fill the matrix, and we read the score in the last corner.
But how do we find the alignment that produces that score?
After we built the matrix, we must go back from the “optimal score” finding which was the path
There may be more than one solution
Some programs build the alignment at the same time they build the matrix, but that requires more memory
GCAT-GCU G-ATTACA
GCA-TGCU G-ATTACA
GCATG-CU G-ATTACA
for i=0 to length(A)
M[i,0] ← -GapPenalty*i
for j=0 to length(B)
M[0,j] ← -GapPenalty*j
for i=1 to length(A)
for j=1 to length(B)
{
Match ← M[i-1,j-1] + S[A[i], B[j]]
Delete ← M[i-1, j] - GapPenalty
Insert ← M[i, j-1] - GapPenalty
M[i,j] ← max(Match, Insert, Delete)
}
AlignmentA ← ""
AlignmentB ← ""
i ← length(A)
j ← length(B)
while (i > 0 or j > 0)
{
if (i > 0 and j > 0 and M[i,j] == M[i-1,j-1] + S[A[i], B[j]])
{
AlignmentA ← A[i] + AlignmentA
AlignmentB ← B[j] + AlignmentB
i ← i - 1
j ← j - 1
}
else ...
... if (i > 0 and M[i,j] == M[i-1,j] - GapPenalty)
{
AlignmentA ← A[i] + AlignmentA
AlignmentB ← "-" + AlignmentB
i ← i - 1
}
else
{
AlignmentA ← "-" + AlignmentA
AlignmentB ← B[j] + AlignmentB
j ← j - 1
}
}
Wikipedia
Wikipedia
| Needleman–Wunsch algorithm | Smith–Waterman algorithm | |
|---|---|---|
| Goal | Optimal Global Alignment | Optimal Local Alignment |
| External Gaps | First row and first column are subject to gap penalty | First row and first column are set to 0 |
| Scoring | Score can be negative | Negative score is set to 0 |
| Traceback | Begin with the cell at the lower right of the matrix, end at top left cell | Begin with the highest score, end when 0 is encountered |
Wikipedia
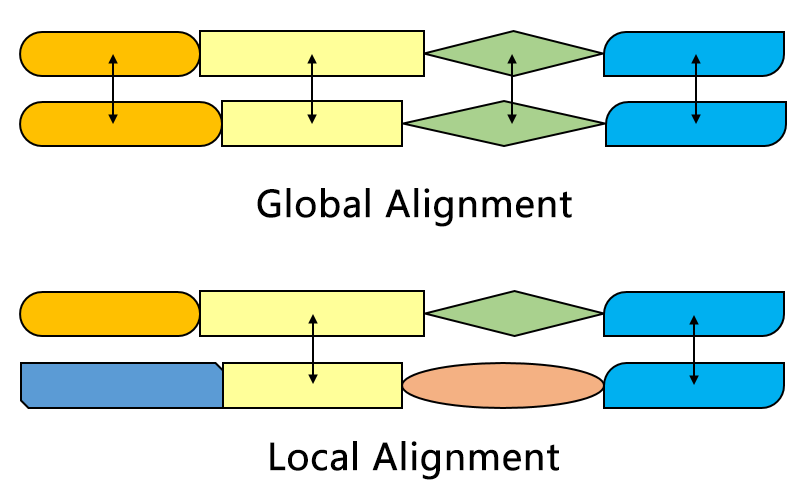
Local alignment can be found using the method proposed by Temple F. Smith and Michael S. Waterman in 1981
Using dynamic programming we fill a matrix M[i,j]
M[i, j] = max(
M[i-1, j-1] + C[q[i], s[j]],
M[i-1, j] - G,
M[i, j-1] - G,
0)
No negative numbers
Using local alignment we can identify conserved regions
In 1992 Steven Henikoff and Jorja Henikoff created new substitution matrices based on local alignment of blocks
BLOcks SUbstitution Matrix
Idea: each protein domain can evolve at different speeds
A R N D C Q E G H I L K M F P S T W Y V B J Z X A 4 -1 -2 -2 0 -1 -1 0 -2 -1 -1 -1 -1 -2 -1 1 0 -3 -2 0 -2 -1 -1 -1 R -1 5 0 -2 -3 1 0 -2 0 -3 -2 2 -1 -3 -2 -1 -1 -3 -2 -3 -1 -2 0 -1 N -2 0 6 1 -3 0 0 0 1 -3 -3 0 -2 -3 -2 1 0 -4 -2 -3 4 -3 0 -1 D -2 -2 1 6 -3 0 2 -1 -1 -3 -4 -1 -3 -3 -1 0 -1 -4 -3 -3 4 -3 1 -1 C 0 -3 -3 -3 9 -3 -4 -3 -3 -1 -1 -3 -1 -2 -3 -1 -1 -2 -2 -1 -3 -1 -3 -1 Q -1 1 0 0 -3 5 2 -2 0 -3 -2 1 0 -3 -1 0 -1 -2 -1 -2 0 -2 4 -1 E -1 0 0 2 -4 2 5 -2 0 -3 -3 1 -2 -3 -1 0 -1 -3 -2 -2 1 -3 4 -1 G 0 -2 0 -1 -3 -2 -2 6 -2 -4 -4 -2 -3 -3 -2 0 -2 -2 -3 -3 -1 -4 -2 -1 H -2 0 1 -1 -3 0 0 -2 8 -3 -3 -1 -2 -1 -2 -1 -2 -2 2 -3 0 -3 0 -1 I -1 -3 -3 -3 -1 -3 -3 -4 -3 4 2 -3 1 0 -3 -2 -1 -3 -1 3 -3 3 -3 -1 L -1 -2 -3 -4 -1 -2 -3 -4 -3 2 4 -2 2 0 -3 -2 -1 -2 -1 1 -4 3 -3 -1 K -1 2 0 -1 -3 1 1 -2 -1 -3 -2 5 -1 -3 -1 0 -1 -3 -2 -2 0 -3 1 -1 M -1 -1 -2 -3 -1 0 -2 -3 -2 1 2 -1 5 0 -2 -1 -1 -1 -1 1 -3 2 -1 -1 F -2 -3 -3 -3 -2 -3 -3 -3 -1 0 0 -3 0 6 -4 -2 -2 1 3 -1 -3 0 -3 -1 P -1 -2 -2 -1 -3 -1 -1 -2 -2 -3 -3 -1 -2 -4 7 -1 -1 -4 -3 -2 -2 -3 -1 -1 S 1 -1 1 0 -1 0 0 0 -1 -2 -2 0 -1 -2 -1 4 1 -3 -2 -2 0 -2 0 -1 T 0 -1 0 -1 -1 -1 -1 -2 -2 -1 -1 -1 -1 -2 -1 1 5 -2 -2 0 -1 -1 -1 -1 W -3 -3 -4 -4 -2 -2 -3 -2 -2 -3 -2 -3 -1 1 -4 -3 -2 11 2 -3 -4 -2 -2 -1 Y -2 -2 -2 -3 -2 -1 -2 -3 2 -1 -1 -2 -1 3 -3 -2 -2 2 7 -1 -3 -1 -2 -1 V 0 -3 -3 -3 -1 -2 -2 -3 -3 3 1 -2 1 -1 -2 -2 0 -3 -1 4 -3 2 -2 -1 B -2 -1 4 4 -3 0 1 -1 0 -3 -4 0 -3 -3 -2 0 -1 -4 -3 -3 4 -3 0 -1 J -1 -2 -3 -3 -1 -2 -3 -4 -3 3 3 -3 2 0 -3 -2 -1 -2 -1 2 -3 3 -3 -1 Z -1 0 0 1 -3 4 4 -2 0 -3 -3 1 -1 -3 -1 0 -1 -2 -2 -2 0 -3 4 -1 X -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 * -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 * A -4 R -4 N -4 D -4 C -4 Q -4 E -4 G -4 H -4 I -4 L -4 K -4 M -4 F -4 P -4 S -4 T -4 W -4 Y -4 V -4 B -4 J -4 Z -4 X -4 * 1
The most common tool for local alignment is BLAST
Basic Local Alignment Search Tool
Uses an index to speed up the lookup of local alignments
You can choose the word size of the index.
BLAST is not Global Alignment