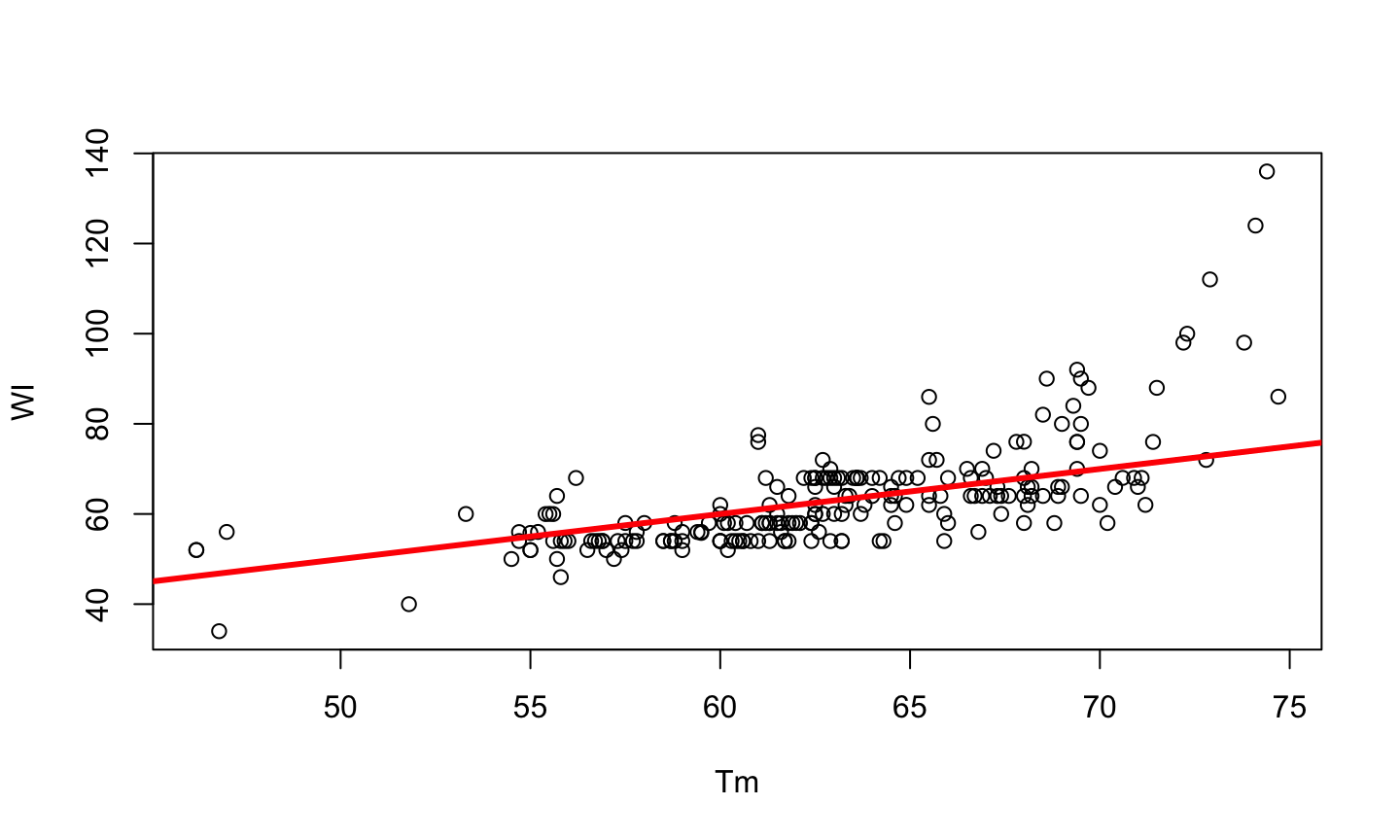
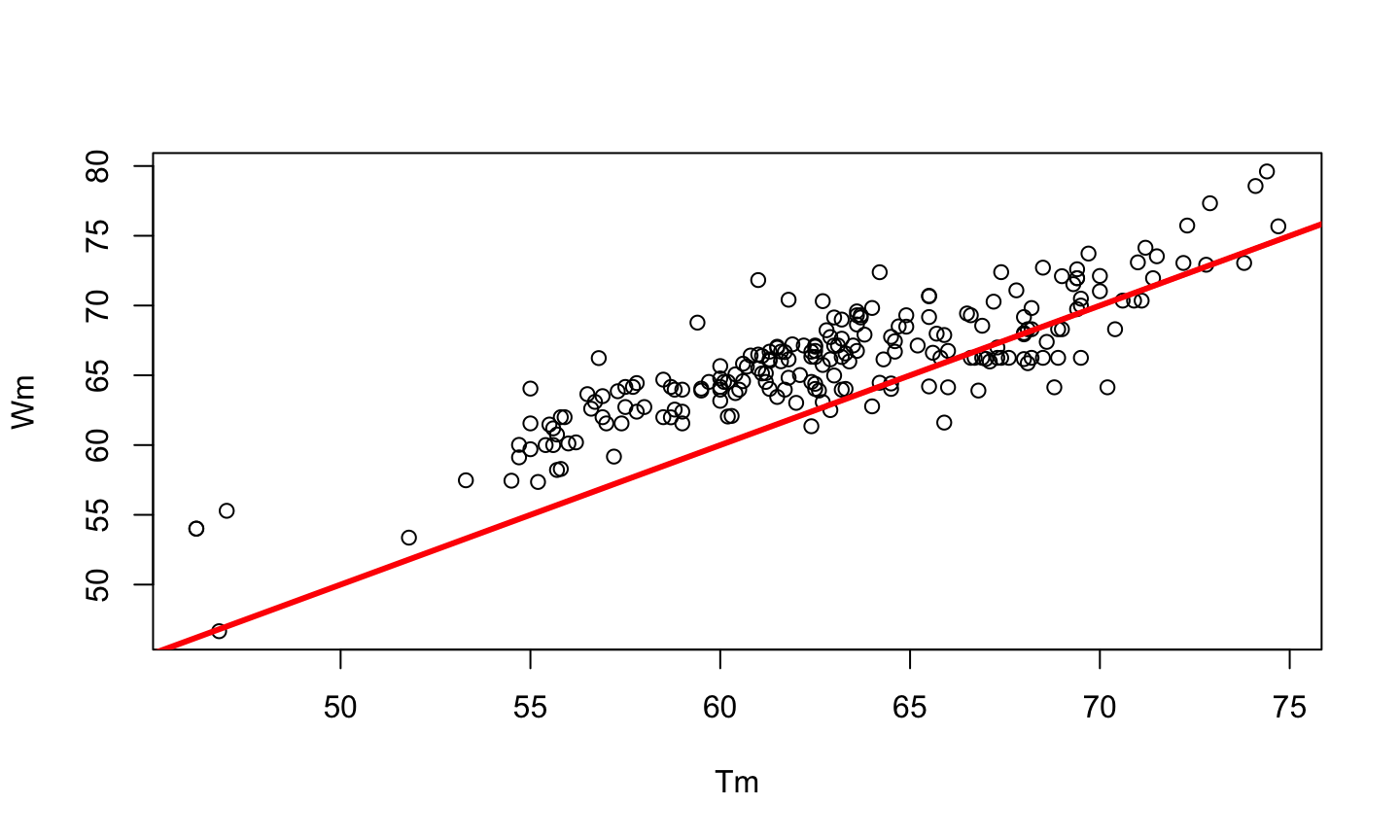
PCR is a method developed by Kary Mullis in the 1980s, used to synthesize millions of copies of a given DNA sequence
PCR is based on separate double-strand DNA using high temperatures, and complementing each DNA single-strand using a polymerase that works at these high temperatures
Taq DNA polymerase, which was isolated from Thermus aquaticus, can polymerize deoxynucleotide precursors (dNTPs) in a temperature range of 75-80oC
Polymerase extends a pre-existing pairing, initially made by primers that bind spontaneously to specific sites on the DNA