23 September 2016

Contents

  • Why math?
  • Descriptive statistics: simple models
  • Linear models
  • Introduction to Probabilities
  • Statistical inference

Why everybody should know math

What is the story here?

  • To understand the story we need to know the language
  • Without the language we only see the pictures and try to guess the meaning
  • “The laws of Nature are written in the language of mathematics”

The universe […] cannot be understood unless one first learns […] the language and interpret the characters in which it is written. It is written in the language of mathematics, […] without these, one is wandering around in a dark labyrinth.

Galileo Galilei (1564 – 1642), Italian astronomer, physicist, engineer, philosopher, and mathematician

Mathematics is not about numbers, equations, computations or algorithms: it’s about understanding

William Paul Thurston (1946 – 2012), American mathematician

The only way to learn mathematics is to do mathematics

Paul Halmos (1916 – 2006) Hungarian-born American mathematician

Math is not Everywhere

  • [Historically] mathematics that makes the most difference to society has been the province of […] few
  • Societies have valued and cultivated math not because it is everywhere and for everyone but because it is difficult and exclusive
  • […] elite mathematics today […] remains a discipline that vests special authority in those who […] are already among our society’s most powerful

Scientific American, August 2016

From big pyramids to big data

  • Political power in ancient Egypt was based on the “god” status of the pharaoh
  • He showed his power by ordering the Nile to grow
  • It worked because he had a model of the seasons
  • Today CEOs have immense power because they have models of people’s behavior
  • “Knowledge is Power”

How do we get knowledge?

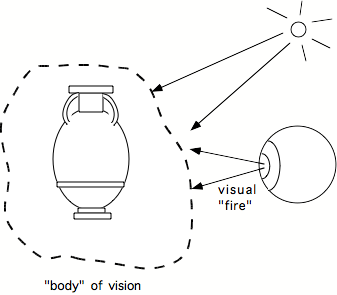
Our senses can fool us

  • Optical illusions: which blue circle is bigger?
  • Dreams
  • Incomplete information: the Earth is flat

We cannot trust 100% our senses

Our mind likes to fool ourselves

  • Poster child: Aristotle
  • We are bad at generalizations

Science: knowledge creation

We combine observations and reasoning

  • We find patterns in observations
  • We describe patterns and relationships with a model
  • Many models are possible
    • Discard models that do not match evidence
    • Prefer simpler models
      • Occam’s razor

Software comes and goes

Math is forever

  • We abstract the question
  • We model the relationships
  • We solve the model (using computers)
  • We interpret the solution back into biology

Software changes every ~5 years

Models last longer

Models

All models are wrong …

“But math is hard…”

Well… it depends

3 x 4

3 x 4 + 5

34 x 45

345 x 456

We have two brains

Two systems of thinking

Daniel Kahneman, 2002 Nobel Memorial Prize in Economic Sciences

Two systems of thinking

System 1

Fast

  • instinctive
  • emotional
  • automatic
  • cheap

System 2

Slow

  • deliberate
  • rational
  • intentional
  • expensive

The priority of our organism is

  1. Survival
  2. Save energy

So System 1 is the default mode

Most of the time we use the cheap intuitive system

Rational thinking (i.e. math) is not spontaneous

Doing math is like running 🏃🏻

  • It requires energy and willpower
  • Everybody can run 10K … if trained correctly