February 23, 2016
Clustering
Understanding by Forgetting
Funes: Someone with perfect memory
For nineteen years he had lived as one in a dream:
- he looked without seeing, listened without hearing, forgetting everything, almost everything.
When he fell, he became unconscious; when he came to, the present was almost intolerable in its richness and sharpness
He can see and remember everything
We, at one glance, can perceive three glasses on a table
Funes, all the leaves and tendrils and fruit that make up a grapevine
He knew by heart the forms of the southern clouds at dawn
and could compare them in his memory with the mottled streaks on a book in Spanish binding he had only seen once
To think is to forget differences
With no effort, he had learned English, French, Portuguese and Latin.
I suspect, however, that he was not very capable of thought.
To think is to forget differences, generalize, make abstractions.
In the teeming word of Funes, there were only details, almost immediate in their presence.
Funes remembers but does not understand
- He was almost incapable of ideas in a general, Platonic sort
- Not only was it difficult for him to comprehend that the generic symbol dog embrace so many unlike individuals of diverse size and form
- it bothered him that the dog at 3:14 (seen from the side) should have the same name as the dog at 3:15 (seen from the front).

To think is to generalize, make abstractions
- Funes was not very capable of thought.
- To think is to forget differences, generalize, make abstractions.
Computers have very good memory, like Funes
Platonic Idealism
An Idea is the essence of an object
- It defines the kind of a thing
- Ideal things are aspatial and atemporal
- they exist independent of time and space
- for example: geometric figures
- The material things we experience are shadow of the Idea
Allegory of the Cave
Plato’s version of The Matrix

We only see shadows
How do we see
We see the same thing from any side

We see the same person from any side

And at any age


Same essence through time


Forgetting more we see classes


Classes: defined by a pattern

We easily recognize humans
Our brains are very good at finding some patterns

Sometimes we overgeneralize 🙂
Pareidolia


Forgetting more: higher classes
Animals

Grouping similars together
Language: forget details

Forgetting even more

![]()


Numbers are abstractions

Abstractions
\[3+5 = 5+3\]
\[9+2 = 2+9\] And then \[x + y = y + x\]
Algebra is a higher level of abstractions
- We have rules that apply to any number. No matter what number
Clustering
Teach the computer to think

Clustering
Forget differences to find common identity
“New Oxford American Dictionary” defines
cluster
|ˈkləstər|noun
- a group of similar objects growing closely together: clusters of grapes.
- a group of people or similar objects positioned or occurring close together: a cluster of antique shops.
- a natural subgroup of a population, used for statistical sampling or analysis.
Used to…
- split all the samples into meaningful classes
- Find the characteristic of each class
- classify all instances into classes
- determine the class of new instances
- determine the number of classes
A Correct Clustering
cellular organism; Eukaryota; Metazoa; Bilateria; Coelomata; Deuterostomia; Chordata; Craniata; Vertebrata; Gnathostomata; Teleostomi; Euteleostomi; Sarcopterygii; Tetrapoda; Amniota; Mammalia; Primates; Hominoidea; Hominidae; Homininae; Homo; H.sapiens; Latinamerican; chilean
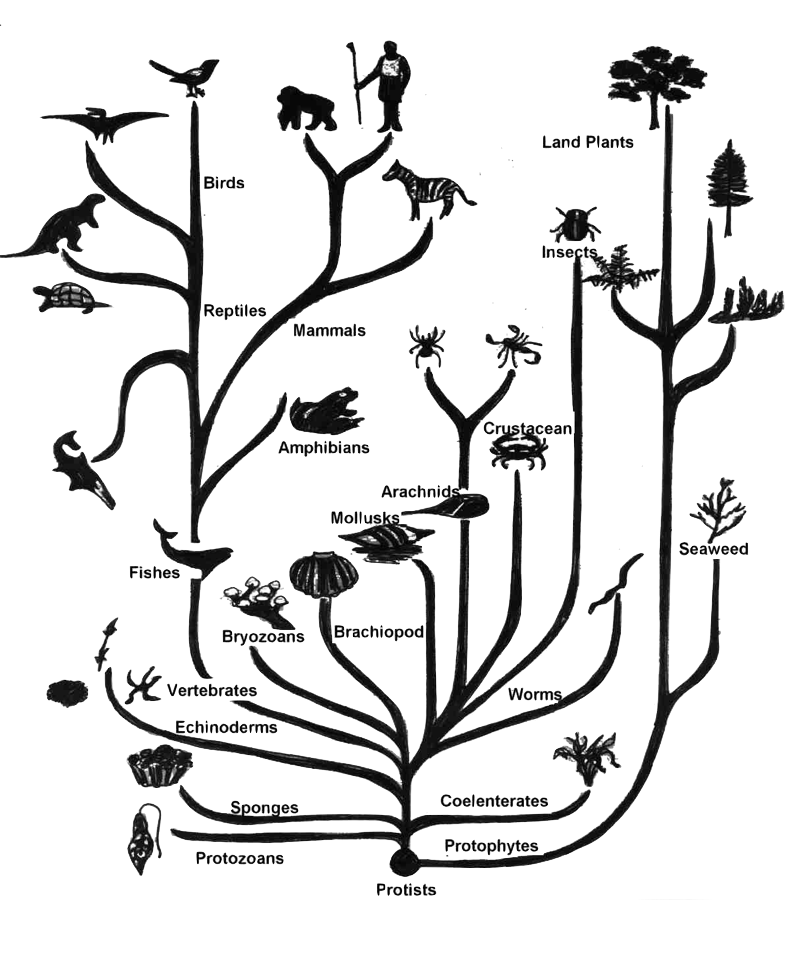
Tree of Life
A Correct Useful Clustering
- Different groupings can be correct at the same time
- The number of clusters depending on the context
- This is called granularity level
- meaning “the size of the grains”
Example
- Variables: Gene Expression
- Individuals: cancer samples
- Clustering shows 4 groups

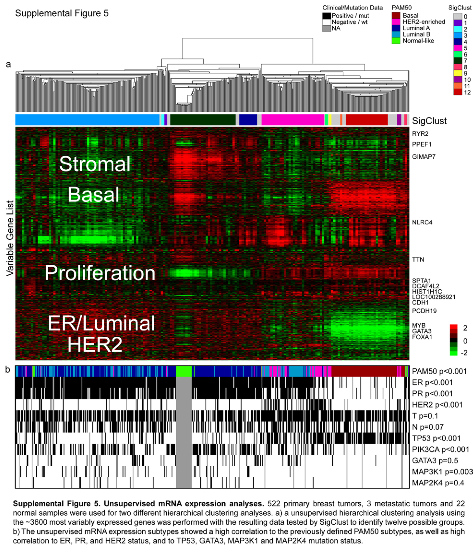
Back to Definition
cluster
|ˈkləstər|noun
- a group of similar objects growing closely together
How do we know when two objects are similar?
Distance: a way to measure differences
Let us put a number to measure similarity
- The distance of 2 things is a non-negative number
- smaller distance means more similar
- distance of a thing to itself is zero \[\mathrm{dist}(x,x)=0\]
- symmetry: \(\mathrm{dist}(x,y)=\mathrm{dist}(y,x)\)
- Triangular inequality \[\mathrm{dist}(x,z)\leq\mathrm{dist}(x,y)+\mathrm{dist}(y,z)\]
Example of distance: \((x-y)^2\)
Here \(x\),\(y\),\(z\) are real numbers, positive or negative.
If \(\mathrm{dist}(x,y)=(x-y)^2\) then:
- \(\mathrm{dist}(x,y)\) is never negative
- \(\mathrm{dist}(x,x)=0\) for any \(x\)
- \(\mathrm{dist}(x,y)=\mathrm{dist}(y,x)\)
- \(\mathrm{dist}(x,z)\leq\mathrm{dist}(x,y)+\mathrm{dist}(y,z)\)
So this is a valid distance
Exercise: prove it
Hierarchical Clustering
bottom up: joining one by one
- if \(\mathrm{dist}(x, y)\) is the smallest distance, we join \(x\) and \(y\)
- we create cluster \(C\)
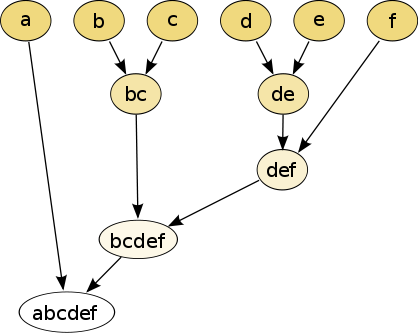
Now we have to measure the distance between elements and clusters
How to measure distance between \(x\) and \(C\)?
How to measure distance between cluster \(C_1\) and \(C_2\)?
Average Linkage
\[\mathrm{dist}(x, C)=\mathrm{mean} (\mathrm{dist}(x, y): y \in C)\] \[\mathrm{dist}(C_1, C_2)=\mathrm{mean} (\mathrm{dist}(x, y): x \in C_1, y \in C_2)\] Distance between two clusters is the distance between their mass centers
Single Linkage
\[\mathrm{dist}(x, C)=\min(\mathrm{dist}(x, y): y \in C)\] \[\mathrm{dist}(C_1, C_2)=\min(\mathrm{dist}(x, y): x \in C_1, y \in C_2)\] Distance between two clusters is the smallest distance between their elements
Complete Linkage
\[\mathrm{dist}(x, C)=\max(\mathrm{dist}(x, y): y \in C)\] \[\mathrm{dist}(C_1, C_2)=\max(\mathrm{dist}(x, y): x \in C_1, y \in C_2)\] Distance between two clusters is the maximal distance between their elements
GEO
library(GEOquery)
se <- getGEO(GEO="GSE3541", destdir = "geo-data")
Accessing expression data
length(se)
[1] 1
se <- se[[1]] expr <- exprs(se) pheno <- pData(se) feature <- fData(se)
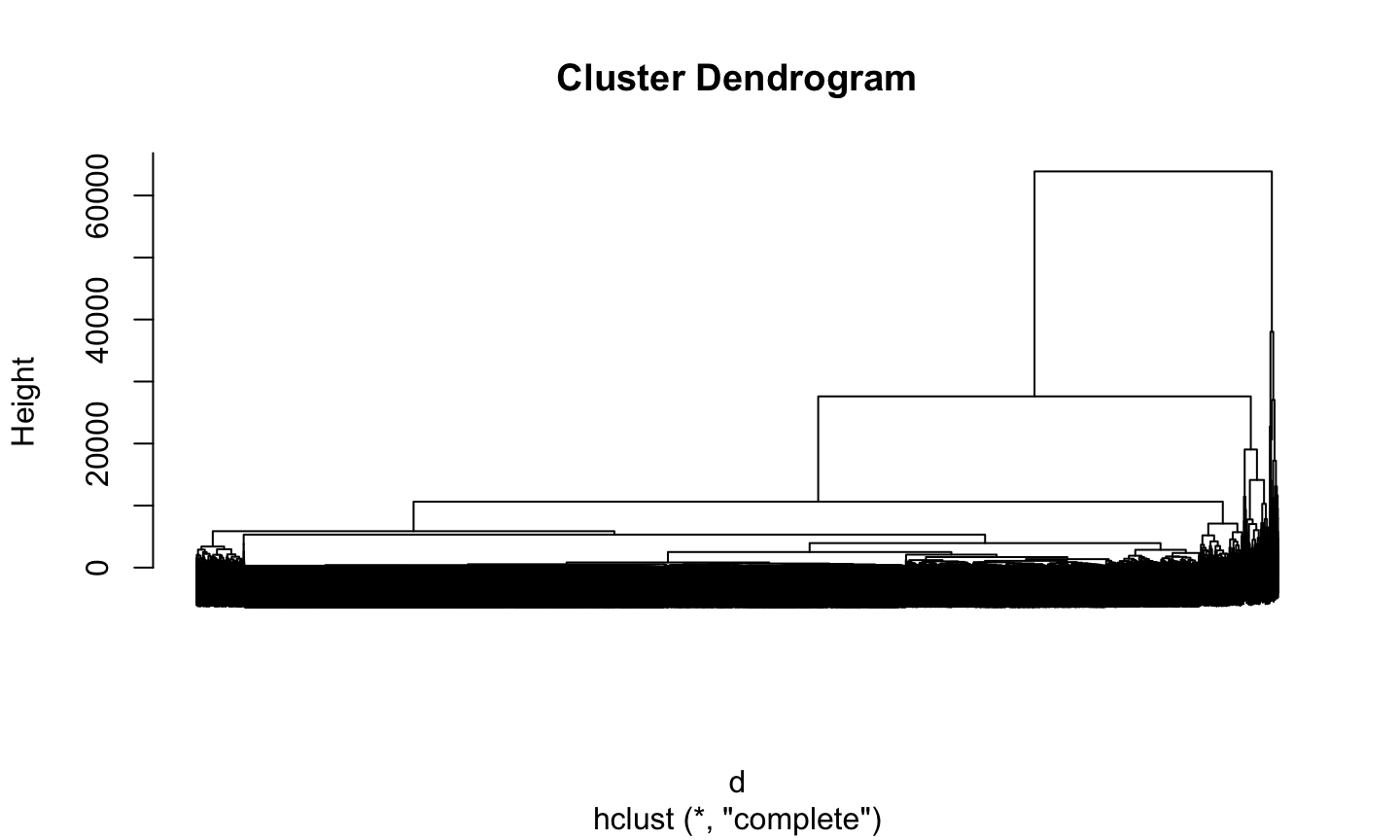
Hierarchical clustering
d <- dist(expr) tree <- hclust(d, method = "complete") plot(tree, labels = FALSE)
Measuring distance between vectors
Euclidean Distance
- square root of the sum of squares
- has a geometrical sense
- “expensive” in computation time
If \(x\) and \(y\) are vectors of length \(n\), then \[\mathrm{dist}_2(x,y)=\sqrt{(x_1-y_1)^2+\cdots +(x_n-y_n)^2}\]
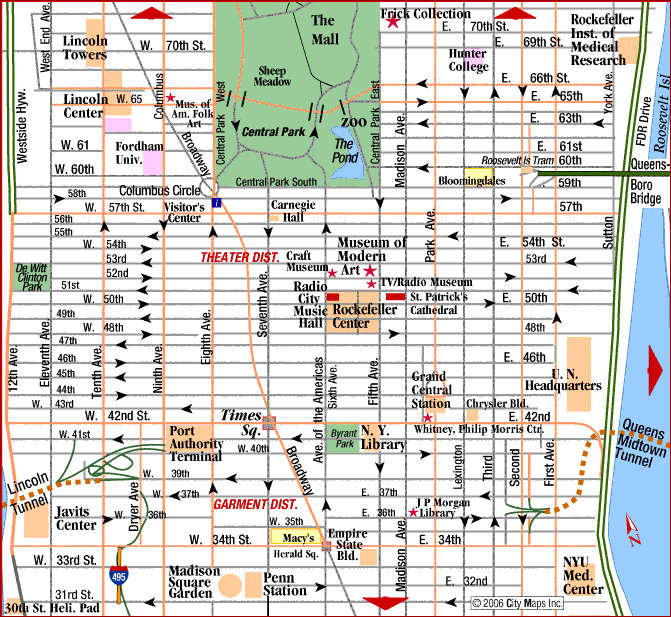
Manhattan Distance
Sum of absolute values \[\mathrm{dist}_1(x,y)=\vert x_1-y_1\vert +\cdots +\vert x_n-y_n\vert\] Different geometrical meaning
Why “Manhattan”?
Maximal Distance
\[\mathrm{dist}_∞ = max(\vert x_1-y_1\vert ,\ldots,\vert x_n-y_n\vert )\] Only the biggest one matters
Example
\[X = (0,0), Y = (100,1)\] \[\mathrm{dist}_1(X,Y) = 101\] \[\mathrm{dist}_2(X,Y) = 100.005\] \[\mathrm{dist}_\infty(X,Y) = 100\]
Example
\[X = (10,1), Y = (100,1)\] \[\mathrm{dist}_1(X,Y) = 90\] \[\mathrm{dist}_2(X,Y) = 90\] \[\mathrm{dist}_\infty(X,Y) = 90\]
Homework
For next class
We will start analyzing genomic sequences.
Prepare slides to explain
- FASTA file
- GFF file
- GenBank file
They are explained in Wikipedia and NCBI website.
Credits of Images
Chair image by Alex Rio Brazil - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=8045709
dogs By
YellowLabradorLooking_new.jpg:derivative work: Djmirko (talk)YellowLabradorLooking.jpg:User:HabjGolden_Retriever_Sammy.jpg:Pharaoh HoundCockerpoo.jpg:ALMMLonghaired_yorkie.jpg:Ed Garcia fromUnited StatesBoxer_female_brown.jpg:Flickr userboxercabMilù_050.JPG:AleRBeagle1.jpg:TobycatBasset_Hound_600.jpg:ToBNewfoundland_dog_Smoky.jpg:Flickr user DanDee Shotsderivative work: December21st2012Freak (talk) -YellowLabradorLooking_new.jpgGolden_Retriever_Sammy.jpgCockerpoo.jpgLonghaired_yorkie.jpgBoxer_female_brown.jpgMilù_050.JPGBeagle1.jpgBasset_Hound_600.jpgNewfoundland_dog_Smoky.jpg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10793219allegry of the cave By Veldkamp, Gabriele and Maurer, Markus - Veldkamp, Gabriele. Zukunftsorientierte Gestaltung informationstechnologischer Netzwerke im Hinblick auf die Handlungsfähigkeit des Menschen. Aachener Reihe Mensch und Technik, Band 15, Verlag der Augustinus Buchhandlung, Aachen 1996, Germany, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=24826744

