Last week we talked about
- why computing is important to us
- what is a computer
- what a computer can do
- some parts of a computer
- some strategies for effective learning
Can you tell something about this?
Last week we talked about
Can you tell something about this?
The most simple answer to a question is yes or no
When we bet on a tossed coin, what do we know?
This elementary information unit is called bit
(binary digit)
It can be represented by on/off, true/false, 0/1, etc.
For technical reasons modern computers handle only packs of 8 bits
That is called a byte and can represent a number in the range 0 to 255
Using two bytes we can represent numbers between 0 and 65535
How? If \(x\) and \(y\) are two bytes, we can evaluate \[x+256 y\]
The idea can be extended to using 4 bytes
0 to 4 294 967 295
and also to using 8 bytes
From 0 to 18 446 744 073 709 551 615 \[1.8466 \cdot 10^{19}\]
With a small modification we can also represent negative numbers.
For example, a number \(x\) between -128 and 127 can be represented as \(x+128\)
Note: in practice we use a similar but different encoding
Two steps: sampling (in time) and discretization (in voltage) 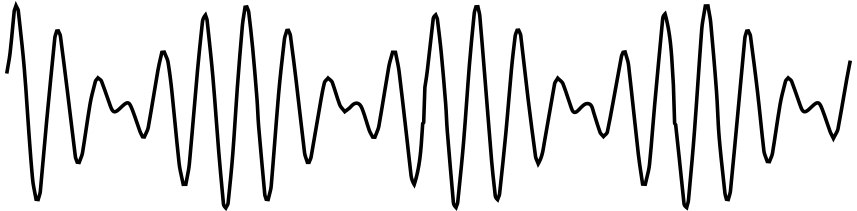

cats
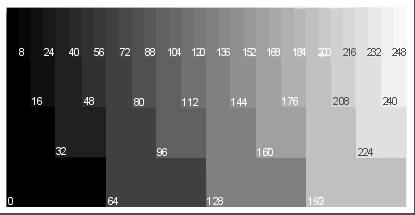
greyscale
Using scientific notation we write \[1.8466 \cdot 10^{19}\] Using the same idea we can use two numbers like this \(x\cdot 2^y\)
There are two versions: single and double precision
They use 4 and 8 bytes, respectively
Notice that this approach has some limitations
Not all numbers are represented exactly
Can also represent special values
The computer has memory to store information. These are electronic devices
When the computer is turned off, the information is lost
We need to copy information to a secondary storage
How much can we store in the computer?
What is the size of the memory of your computer?
What is the size of the disk?
The memory (RAM) is like a desk.
The disk is like a book shelf.
The most natural way to represent a text document is to encode each letter with a single byte
There is a basic standard for English, called ASCII
Each number from 0 to 127 is either a symbol or a special signal, such as
| 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ( | 2 | < | F | P | Z | d | n | x | |
| 1 | ) | 3 | = | G | Q | \[| e | o | y 2| | | 4| >| H| R|\\| f | p | z 3| !| +| 5| ?| I| S|\] | g | q | { | |
| 4 | " | , | 6 | @ | J | T | ^ | h | r | | |
| 5 | # | - | 7 | A | K | U | i | s | } | |
| 6 | $ | . | 8 | B | L | V | ` | j | t | ~ |
| 7 | % | / | 9 | C | M | W | a | k | u | |
| 8 | & | 0 | : | D | N | X | b | l | v | |
| 9 | ´ | 1 | ; | E | O | Y | c | m | w |
Numbers between 128 and 255 are not used in ASCII
Non English languages use these values for symbols like “Ç”, “Ö”, “É”, “Ñ”
Microsoft Word files (doc or docx) are NOT text files
Thou shall not use Word for this course