1. Medieval space science

The Earth circumference is known since Eratosthenes, looking at the shadows of a vertical rod, measured the angle of the sun in two different cities (Alexandria and Syene, today called Assuan) on the same day, circa 240 BCE. Knowing the distance between the cities, he estimated the Earth circumference with about 15% of difference with the actual value. As a reference, 1700 years later Columbus was mistaken by 25%. The WikiPedia entry for Earth’s circumference describes also other methods used in ancient times for this measurement.

One issue with this estimation is that it assumes that the earth is a sphere, but in reality the equatorial radius is larger than the polar one. The history of how people realized this is also interesting, as you can read on the wikipedia entry for the French Geodesic Mission to the EquatorIn that article there is an interesting note about the usage of a “seconds pendulum” as a measure of distance, which happens to be very near one meter. I read somewhere that the meter was chosen because it was near the “seconds pendulum”.

. Nevertheless, it is useful to remember that the original definition of a meter was such that the Earth circumference was 40 thousand kilometers. This easy-to-remember value has an error of less than 0.2%.

Around the eleventh century, the Spanish Arab Abū ʿAbd Allāh Muhammad ibn Mucādh al-Jayyānī Usually shortened as ibn Mucādh. I like the name al-Jayyānī, meaning “from Jaén”, a city in Andalucía. Since I live in Kadıköy, I also like that he worked as a qādi (judge).

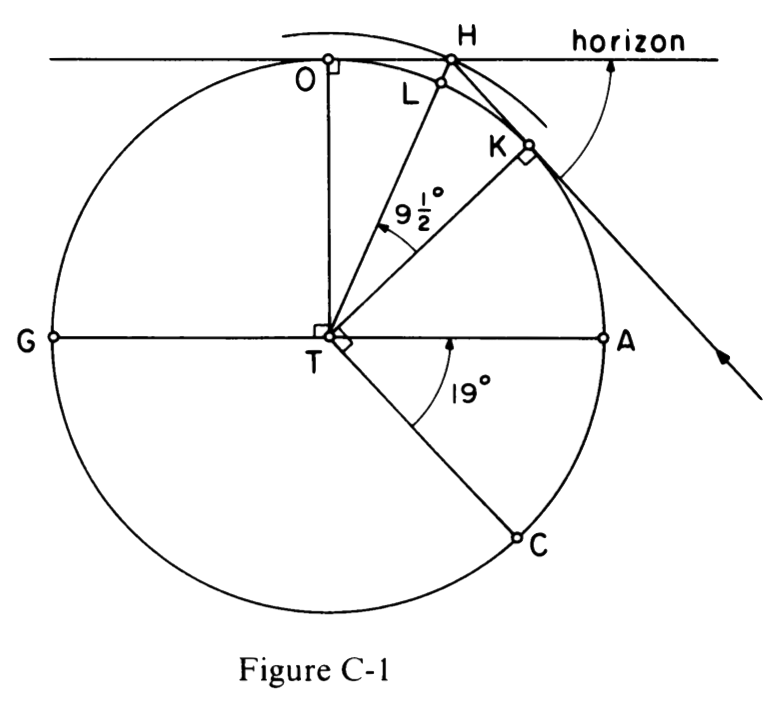
wrote the text “On Twilight and the Rising of Clouds” in which he used the sunset and twilight times to determine “the height of the clouds”. Today we would call that “the height of the atmosphere”. By knowing the time between sunset and total darkness (or between daybreak and sunrise) he calculated the angle θ that the Earth rotated, and thus, using trigonometry, found that \[\frac{TK}{TH}=\frac{r}{r+x}=\cos(θ/2)\] where \(r\) is the Earth’s radius and \(x\) is the atmosphere’s height. For more details see the following illustration, taken from a paper by Goldstein (1977)Goldstein, B. R. (1977), “Ibn Mucādh’s Treatise On Twilight and the Height of the Atmosphere”, Archive for History of Exact Sciences, http://www.jstor.org/stable/41133483.

.

The paper says “twilight was often considered by his Muslim predecessors because of their importance in determining the prayer time”. Notice that in the figure they use 19° for what we call θ, but we can use the “Istanbul pray times” to calculate it.

Calculate the height of the atmosphere with the corresponding margin of uncertainty. Assume that the uncertainty are small and use the statistical uncertainty formulas.
(Bonus) How could we replicate Eratosthenes’ experiment using cellphones, the internet, and all modern technology available on any house?

Remember that \[\frac{d\cos\theta}{d\theta}=-\sin\theta\]

2. Kapadokya

Please provide confidence intervals for the following values.

How many balloons fly every day in Kapadokya?
Balloons can only fly when there is not too much wind or rain. How many days can the fly every year?
How many tourists flies every day? How much do they pay in total?
How much money does this business produce?
What is the volume of air inside one of these balloons?
What is the temperature inside the balloon?

I have some intuition for these values, so we can discuss them.

3. Is this Science?

In the second part of our course we have discussed “Good Practices for Project Management”. Is this science? How can we make it more “scientific”?