Please download the file homework11.R and write your results there. Send the your answers to my mailbox.
1. GC content
Now that we have more powerful tools, we will explore again the GC content of Carsonella rudii. First, we will see that GC content can be seen as the average of an event.
1.1 Is this nucleotide G or C?
Please write a function called is_G_or_C that determines
if a nucleotide is either “G” or “C”. The function
takes a character vector (called dna) and returns
a logic vector called ans. If dna[i]
is “G”, “g”, “C” or “c”, then ans[i] is
TRUE, otherwise it is FALSE.
is_G_or_C <- function(dna) {
# write here
}Test your function with the following code:
is_G_or_C(c("a","c","t","g"))[1] FALSE TRUE FALSE TRUEis_G_or_C(c("A","C","T","G"))[1] FALSE TRUE FALSE TRUEmean(is_G_or_C(c("A","C","T","G")))[1] 0.5As you can see, the GC content can be seen as the mean of
the event is_G_or_C(). It is natural to think that we can
also calculate the variance and the standard deviation. How can we do
that?
1.2 Simulating some genes
We will use this function over simulated data. We need 100 genes of
different lengths. Please create a vector, called
sim_gene_length, with 100 elements taken randomly (with
replacement) from the values 100, 103, 106, …, 1201. Then create a
list, called sim_genes, with “random DNA
sequences”Notice that sim_gene_length is a
vector, since all elements are numbers. On the other side
sim_genes has to be a list, since every element is
itself a vector, and each one can have different length. We cannot
handle this kind of data in a vector, it has to be a list.
. Each element sim_genes[[i]] must be a
random character vector with length sim_gene_length[i].
Only the letters “A”,“C”,“G”, and “T” are valid, and all have the same
probability.
After you have created sim_genes, calculate the
mean of is_G_or_C() for each gene and store them
in the vector sim_mean_GC. You also need to calculate the
variance of is_G_or_C() for each gene and store
the result in sim_var_GC.
Finally, calculate the standard error of the mean by taking
the square root of sim_var_GC divided by
sim_gene_length, and store it in
sim_std_err_mean.
# write hereTest your results with this code:
par(mfrow=c(2,2))
hist(sim_mean_GC, col="grey")
hist(sim_var_GC, col="grey")
hist(sim_gene_length, col="grey")
hist(sim_std_err_mean, col="grey")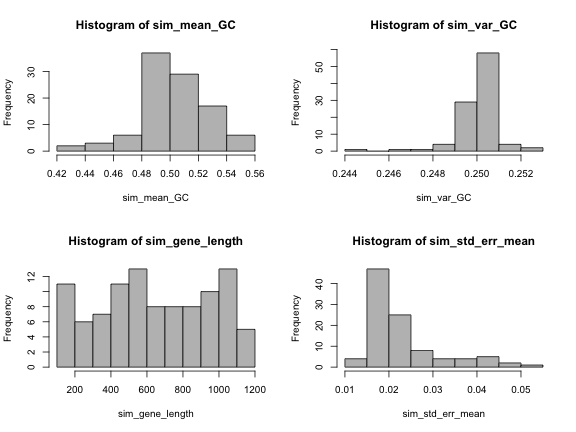
1.3 Genes versus genome
Since all genes are taking from a random population, and all
nucleotides have the same probability, then in this
case we know that the genome GC contentdo you agree?
is 0.5.
But in many cases we do not have the full genome, just some genes. We want use the information of each gene to build a confidence interval for the genome GC content.
Fortunately we know that, if the genes are random DNA sequences, the
GC content of the genes is not too different from the GC content of the
genomeWe know this because GC content is an average so they
obey the Law of Large Numbers.
. Moreover, we know that the GC content of the genes is a
random variable following the Normal distributionThis is true because of the Central Limit
Theorem.
.
Unfortunately, we do not know the standard deviation of the
population (we are using each gene as a sample). Instead, we can
approximate it with the standard error of each geneStandard error of the sample is the standard deviation
of the sample divided by the square root of the sample size \[\sqrt{\frac{\text{var}(x)}{\text{length}(x)}}\]
, but we will have to use the Student’s t
distribution.
We start by choosing the confidence level \(1-\alpha=95\%\), therefore
alpha is 0.05. You must use the function qt()
to find the number of standard errors k that will
give you the confidence interval. Remember that the number of
degrees of freedom is sim_gene_length-1.
Then you must calculate the vectors sim_lower, with the
lower limits of each confidence interval, and sim_upper,
with the upper limits.
alpha <- 0.05
# write hereNow you can count how many of the confidence intervals really contained the real value. In other words, you can see how good was the prediction.
mean(sim_lower <= 0.5 & 0.5 <= sim_upper)[1] 0.96You can see your results with this code:
gene_order <- 1:length(sim_genes)
plot(gene_order, sim_mean_GC, pch=16, ylim=c(0.3, 0.7))
arrows(gene_order, sim_upper, gene_order, sim_lower,
angle=90, code=3, length = 0.02)
abline(h=0.5, col="red")
The previous plot is hard to see, because there is a lot of
variability. It can be a little easier if we use the function
order() to sort the values, as in the following code:
sorted <- order(sim_mean_GC)
plot(gene_order, sim_mean_GC[sorted], pch=16, ylim=c(0.3, 0.7))
arrows(gene_order, sim_upper[sorted], gene_order, sim_lower[sorted],
angle=90, code=3, length = 0.02)
abline(h=0.5, col="red")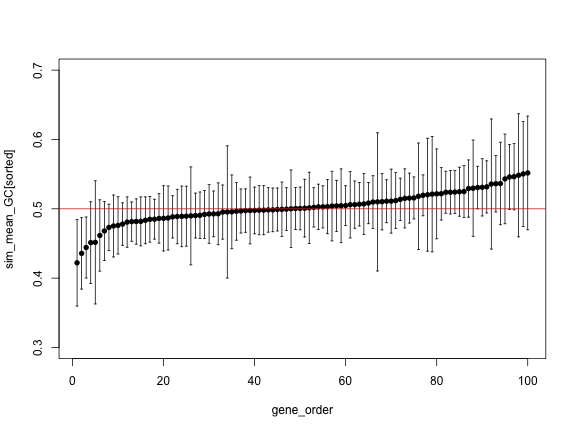
2. Apply to real data
Now we will use this function over the genes of Carsonella rudii.
2.1 Read the genes from a file
Please download the file c_rudii.fna.txt
and save it in your computer. It has to be stored in your computer to be
fast and efficient.
Using the library seqinr, please write the code to
- read the FASTA file and load all genes in a list called
genes, - calculate the mean of
is_G_or_C()for each gene, and store each value in a vector calledmean_is_G_or_C. The length of this vector must be the number of genes - calculate the variance of
is_G_or_C()for each gene, and store each value in a vector calledvar_is_G_or_C. - calculate the length of each gene, and store each value in a vector
called
gene_length. - calculate the standard error of the mean for each gene. That is, the square root of the variance divided by the gene length.
# write hereTest your results with this code:
length(genes)[1] 182par(mfrow=c(2,2))
hist(mean_is_G_or_C, col="grey")
hist(var_is_G_or_C, col="grey")
hist(gene_length, col="grey")
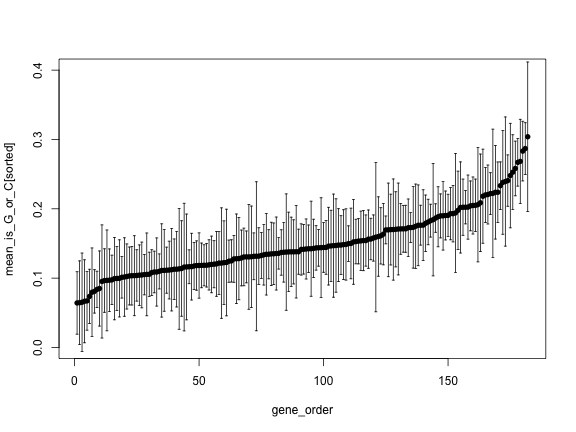
hist(std_err_mean, col="grey")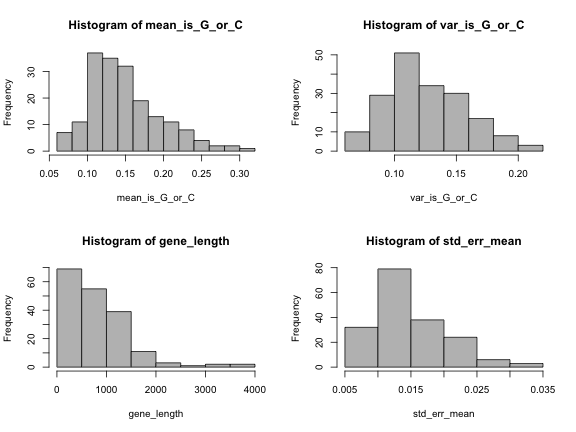
2.2 Using genes to estimate genome GC content
We want use the information of the real genes to build a confidence interval for the genome GC content.
Since the values have much more variability than in the simulation,
we choose a confidence level of \(1-\alpha=99.9\%\), therefore
alpha is 0.001. You must use the function qt()
to find the number of standard errors k that will
give you the confidence interval. Remember that the number of
degrees of freedom is gene_length-1.
Then you must calculate the vectors lower, with the
lower limits of each confidence interval, and upper, with
the upper limits.
alpha <- 0.001
# write hereTest your results with this code:
gene_order <- 1:length(genes)
plot(gene_order, mean_is_G_or_C, pch=16, ylim=c(0, 0.4))
arrows(gene_order, upper, gene_order, lower,
angle=90, code=3, length = 0.02)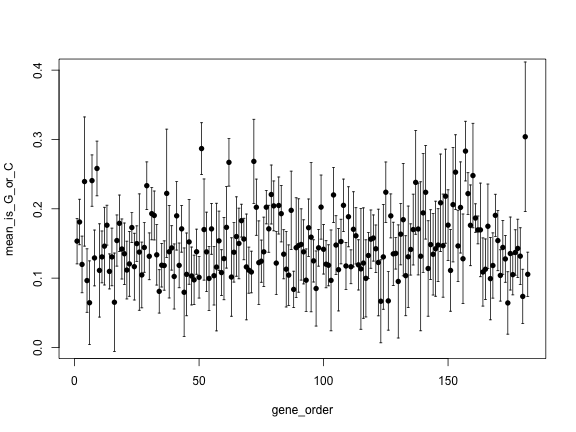
The previous plot is hard to see, because there is a lot of
variability. It can be a little easier if we use the function
order() to sort the values, as in the following code:
sorted <- order(mean_is_G_or_C)
plot(gene_order, mean_is_G_or_C[sorted], pch=16, ylim=c(0, 0.4))
arrows(gene_order, upper[sorted], gene_order, lower[sorted],
angle=90, code=3, length = 0.02)