Today on Class 13 we saw an interesting system that has very different behavior depending on the rate parameter. This system was discovered in modeling of insect population, in particular when there is super-population (see Utilda 1957). It is called “Quadratic Map”.

You can see the system drawing in the slide 17 of class 13. We can simulate the system with the following function, which you can use for this homework.

quad_map <- function(N, A, x_ini) {
  x <- rep(NA, N)
  x[1] <- x_ini
  for(i in 2:N) {
    x[i] <- A * x[i-1] * (1 - x[i-1])
  }
  return(x)
}

As we discussed in class, the initial condition is not very important, since the long time behavior is an attractor. The result will be the same as long as x_ini is strictly between 0 and 1. For this exercise you can use x_ini=0.5.

The really important part is the effect of the rate A. It can take values between 0 and 4, but the most interesting behaviors are observed for A between 2.9 and 3.999999.

Your first mission is to build a vector a_values with numbers from 2.9 to 4 incrementing by 0.001.

Then you have to draw an “empty” plot with horizontal axis from 2.9 to 4, and vertical axis from 0 to 1. You can plot anything or use the xlim= and ylim= options, but make sure that the plot area is clean. For example you can use the option type="n".

Now, for each value of a_values you have to simulate quad_map() for 1500 steps. The first 1000 steps are transient. You have to draw the last 500 steps in the same plot. Since there are many points, use pch=".".

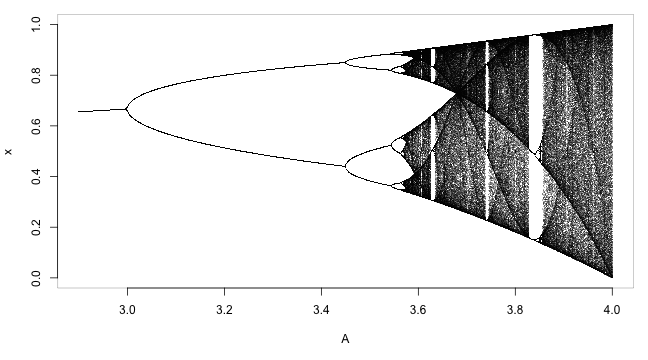
The result should look like this:

Notice that in quad_map(), the inputs are numbers, not vectors. That is, you can say quad_map(N=100, A=2, x_ini=0.5) but you cannot say quad_map(N=50:100, A=a_values, x_ini=c(0.5, 0.6, 0.4). Only single values.

For extra points you can choose a color that is semi-transparent. For example you can use “black” with alpha channelOf course you can use Google to find the meaning of alpha channel and how to use it on R. Maybe something like “How to change the alpha value of colours in R”. You should use Google for anything that you don’t understand.

equal to 0.3.

#'---
#'title: "Homework 3 - CMB2"
#'author: "Your Name"
#'number: Your Number
#'date: "when you send it"
#'---